��Ŀ����
6����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ԲC�䣺x2+y2=1����ԲC���϶�����ҽ��㣮��1������ԲC�ı����̺������ʣ�
��2����ֱ֪��l����ԲCֻ��1�����㣬̽�����Ƿ������������P��x1��0����Q��x2��0������x1��x2��ʹ��P��Q��ֱ��l�ľ���֮��Ϊ1��������ڣ������������������ꣻ��������ڣ�˵�����ɣ�
���� ��1��������ɵ�b=c=1��a=$\sqrt{2}$�������õ�C�ı����̺������ʣ�
��2���������ۣ�����ֱ��l����ԲC��ֻ��һ�������㣬ȷ��k��p�Ĺ�ϵ������x���ϴ������㣨s��0������t��0����ʹ�䵽ֱ��l�ľ���֮��Ϊ1���������̣�������ý��ۣ�
��� �⣺��1�������⣬b=c=1��a=$\sqrt{2}$��
����ԲC�ı�����$\frac{{x}^{2}}{2}+{y}^{2}$=1��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��
��2�����ٵ�ֱ��lб�ʴ���ʱ����ֱ��l����Ϊy=kx+p��
������Բ���̵ã�1+2k2��x2+4kpx+2p2-2=0��
��Ϊֱ��l����ԲC��ֻ��һ�������㣬
���ԡ�=16k2p2-4��1+2k2����2p2-2��=8��1+2k2-p2��=0��
��1+2k2=p2��
����x���ϴ������㣨s��0������t��0����ʹ�䵽ֱ��l�ľ���֮��Ϊ1��
��$\frac{|ks+p|}{\sqrt{1+{k}^{2}}}•\frac{|kt+p|}{\sqrt{1+{k}^{2}}}$=1��
����st+1��k+p��s+t��=0��*������st+3��k2+��s+t��kp+2=0 ��**����
�ɣ�*�����������$\left\{\begin{array}{l}{st+1=0}\\{s+t=0}\end{array}\right.$��$\left\{\begin{array}{l}{s=1}\\{t=-1}\end{array}\right.$����$\left\{\begin{array}{l}{s=-1}\\{t=1}\end{array}\right.$��
����**�����������
�ڵ�ֱ��lб�ʲ�����ʱ��ֱ�߷���Ϊx=��$\sqrt{2}$ʱ��
���㣨-1��0����F2��1��0����ֱ��l�ľ���֮��d1?d2=��$\sqrt{2}$-1����$\sqrt{2}$+1��=1��
���ϣ������������㣨1��0������-1��0����ʹ�䵽ֱ��l �ľ���֮��Ϊ��ֵ1��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ�����������������о�������ѧ���ļ���������ͬʱ����ѧ�������������������������е��⣮

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�| A�� | m1=-1��m2=1 | B�� | m=1 | C�� | m=-1 | D�� | �� |
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
| A�� | 4�� | B�� | $\frac{7��}{2}$ | C�� | $\frac{5��}{2}$ | D�� | 3�� |
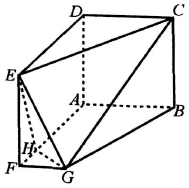 �ڶ�����ABCDEFG�У��ı���ABCD��ADEF�DZ߳���Ϊa�������Σ��ı���ABGH��ֱ�����Σ�AB��AF����FA=2FG=4FH��
�ڶ�����ABCDEFG�У��ı���ABCD��ADEF�DZ߳���Ϊa�������Σ��ı���ABGH��ֱ�����Σ�AB��AF����FA=2FG=4FH�� ��ͼ��ʾ��һ�θ�ӽ�����ϣ���λ��ίΪijѡ�ִ���ķ����ľ�Ҷͼ������λ����86��
��ͼ��ʾ��һ�θ�ӽ�����ϣ���λ��ίΪijѡ�ִ���ķ����ľ�Ҷͼ������λ����86��