题目内容
(1)已知直线x+y=a与圆x2+y2=4交于A,B两点,且|
+
|=|
-
|其中O为坐标原点,求a的值;
(2)圆C的方程为(x-2)2+y2=4,圆M的方程为(x-2-5cosθ)2+(y-5sinθ)2=1,过圆M上任意一点P作圆C的两条切线PE,PF,切点分别是E,F,求
•
的最小值.
| OA |
| OB |
| OA |
| OB |
(2)圆C的方程为(x-2)2+y2=4,圆M的方程为(x-2-5cosθ)2+(y-5sinθ)2=1,过圆M上任意一点P作圆C的两条切线PE,PF,切点分别是E,F,求
| PE |
| PF |
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设A(x1,y1),B(x2,y2).联立直线x+y=a与圆x2+y2=4,化为2x2-2ax+a2-4=0.△>0.得到根与系数的关系,利用|
+
|=|
-
|,可得x1x2+y1y2=0,代入计算即可;
(2)由两圆的圆心距|CM|=5大于两圆的半径之和可得两圆相离,则
•
的最小值是
•
,利用
两个向量的数量积的定义求出
•
的值,即为所求.
| OA |
| OB |
| OA |
| OB |
(2)由两圆的圆心距|CM|=5大于两圆的半径之和可得两圆相离,则
| PE |
| PF |
| HE |
| HF |
两个向量的数量积的定义求出
| HE |
| HF |
解答:
 解:(1)设A(x1,y1),B(x2,y2).
解:(1)设A(x1,y1),B(x2,y2).
联立直线x+y=a与圆x2+y2=4,化为2x2-2ax+a2-4=0.
△=4a2-8(a2-4)=4(8-a2)>0.(*).
∴x1+x2=a,x1x2=
.
∵|
+
|=|
-
|.
∴x1x2+y1y2=x1x2+(a-x1)(a-x2)=0,
∴a2-4-a2+a2=0,
解得a=±2,满足(*).
(2)(x-2)2+y2=4的圆心C(2,0),半径等于2,
圆M (x-2-5cosθ)2+(y-5sinθ)2=1,
圆心M(2+5cosθ,5sinθ),半径等于1.
∵|CM|=5>2+1,故两圆相离.
∵
•
=|
|•|
|•cos∠EPF,要使
•
最小,需|
|、|
|最小,且∠EPF 最大,
如图所示,设直线CM 和圆M交于H、G两点,则
•
的最小值是
•
.
|H C|=|CM|-1=5-1=4,|H E|=
=2
,
sin∠CHE=
=
,
∴cos∠EHF=cos2∠CHE=1-2sin2∠CHE=
,
∴
•
=|H E|•|H E|•cos∠EHF=2
×2
×
=6,
 解:(1)设A(x1,y1),B(x2,y2).
解:(1)设A(x1,y1),B(x2,y2).联立直线x+y=a与圆x2+y2=4,化为2x2-2ax+a2-4=0.
△=4a2-8(a2-4)=4(8-a2)>0.(*).
∴x1+x2=a,x1x2=
| a2-4 |
| 2 |
∵|
| OA |
| OB |
| OA |
| OB |
∴x1x2+y1y2=x1x2+(a-x1)(a-x2)=0,
∴a2-4-a2+a2=0,
解得a=±2,满足(*).
(2)(x-2)2+y2=4的圆心C(2,0),半径等于2,
圆M (x-2-5cosθ)2+(y-5sinθ)2=1,
圆心M(2+5cosθ,5sinθ),半径等于1.
∵|CM|=5>2+1,故两圆相离.
∵
| PE |
| PF |
| PE |
| PF |
| PE |
| PF |
| PE |
| PF |
如图所示,设直线CM 和圆M交于H、G两点,则
| PE |
| PF |
| HE |
| HF |
|H C|=|CM|-1=5-1=4,|H E|=
| |HC|2-|CE|2 |
| 3 |
sin∠CHE=
| |CE| |
| |CH| |
| 1 |
| 2 |
∴cos∠EHF=cos2∠CHE=1-2sin2∠CHE=
| 1 |
| 2 |
∴
| HE |
| HF |
| 3 |
| 3 |
| 1 |
| 2 |
点评:本题考查直线与圆、两圆的位置关系,两圆的切线,两个向量的数量积的定义,二倍角的余弦公式,体现了数形结合的数学思想,判断
•
的最小值是
•
是解题的关键,属于中档题.
| PE |
| PF |
| HE |
| HF |

练习册系列答案
相关题目
定义在R上的偶函数f(x),满足f(x+2)=f(x),且在区间[-1,0]上为递增,则( )
A、f(
| ||
B、f(2)<f(3)<f(
| ||
C、f(3)<f(2)<f(
| ||
D、f(3)<f(
|
方程
-
=1表示椭圆,则α的取值范围是( )
| x2 |
| 3 |
| y2 | ||
sin(2α+
|
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、2kπ+
|
在△ABC,边a、b所对的角分别为A、B,若cosA=-
,B=
,b=1,则a=( )
| 3 |
| 5 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=1-2sinx(sinx+
cosx)的图象向右平移
个单位得函数g(x)的图象,则函数g(x)的解析式是( )
| 3 |
| π |
| 3 |
A、g(x)=2sin(2x-
| ||
| B、g(x)=2cos2x | ||
C、g(x)=2cos(2x+
| ||
D、g(x)=2sin(2x+
|
下列说法错误的是( )
| A、y=x4+x2是偶函数 |
| B、偶函数的图象关于y轴成轴对称 |
| C、奇函数的图象关于原点成中心对称 |
| D、y=x3+x2是奇函数 |
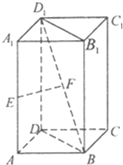 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.