题目内容
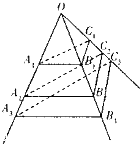如图，互不相同的点A1，A2，…An，…，B1，B2，…，Bn，…C1，C2，…，Cn，…分别在以O为顶点的三棱锥的三条侧棱上，所有平面AnBnCn相互平行，且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等，设OAn=an，若a1=| 3 | 2 |
| A、7 | B、8 | C、9 | D、10 |
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：本题是选择题，可以采取特殊法解答，不妨令OA1⊥平面AnBnCn，并且AnBn⊥AnCn，然后求解几何体的体积，推出a86即可．
解答：
解：不妨令OA1⊥平面AnBnCn，并且AnBn⊥AnCn，
∵OAn=an，若a1=
，a2=2．∴VO-A1B1C1=
×
×
×
×
=
．
∴VA2B2C2-A1B1C1=
×
×2×2×2-
×
×
×
×
=1，
VO-A86B86C86=
+85=
．
又VO-A86B86C86=
×
×a863，
∴
×
×a863=
，
解得：a86=8．
故选：B．
∵OAn=an，若a1=
| 3 | 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |
| 1 |
| 3 |
∴VA2B2C2-A1B1C1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |
VO-A86B86C86=
| 1 |
| 3 |
| 256 |
| 3 |
又VO-A86B86C86=
| 1 |
| 3 |
| 1 |
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 256 |
| 3 |
解得：a86=8．
故选：B．
点评：本题考查特殊值法求解几何体的体积，棱长的求法，如果利用一般法求解，难度比较大，考查了推理能力和计算能力．
练习册系列答案
相关题目
已知数列{an}的前四项为1，3，5，7，…，则下列可以做为该数列通项的是（ ）
| A、n |
| B、2n+1 |
| C、2n-1 |
| D、2n-1 |
正六边形ABCDEF，且
=
，
=
，下列向量可表示为-
+
的是（ ）
| AC |
| a |
| BD |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
椭圆
+
=1（a＞b＞0）的左右焦点F1（-c，0），F2（c，0），c＞0，过F1作圆O：x2+y2=
的切线，切点为E，延长F1E交椭圆于点P，若
=
（
+
），则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| 4 |
| OE |
| 1 |
| 2 |
| OF1 |
| OP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=
sin（
-
）的一个单调增区间为（ ）
| 3 |
| x |
| 2 |
| π |
| 4 |
A、（
| ||||
B、（-
| ||||
C、（-
| ||||
D、（
|
A∉α，过A作与α平行的直线可作（ ）
| A、不存在 | B、一条 |
| C、四条 | D、无数条 |
已知定义在R上的函数y=f（x）对任意的x满足f（x+1）=-f（x），当-1≤x＜1时，f（x）=x3．函数g（x）=
若函数h（x）=f（x）-g（x）在[-6，+∞）上有6个零点，则实数a的取值范围是（ ）
|
A、（0，
| ||||
B、[
| ||||
C、[
| ||||
D、（
|