题目内容
椭圆
+
=1(a>b>0)的左右焦点F1(-c,0),F2(c,0),c>0,过F1作圆O:x2+y2=
的切线,切点为E,延长F1E交椭圆于点P,若
=
(
+
),则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| 4 |
| OE |
| 1 |
| 2 |
| OF1 |
| OP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:判断出E为PF的中点,据椭圆的特点知原点O为两焦点的中点;利用中位线的性质,求出PF2的长度及判断出PF2垂直于PF;通过勾股定理得到a,c的关系,求出椭圆的离心率.
解答:
解:∵
=
(
+
),
∴E为PF1的中点,∴PF2=2OE=b
∵E为切点,
∴OE⊥PF1,
∴PF2⊥PF1,
∵PF1+PF2=2a
∴PF1=-PF2+2a=-b+2a
在Rt△PF1F′中,PF12+PF22=F1F22
即b=
a,
∴c=
=
a,
∴离心率e=
=
.
故选:B.
| OE |
| 1 |
| 2 |
| OF1 |
| OP |
∴E为PF1的中点,∴PF2=2OE=b
∵E为切点,
∴OE⊥PF1,
∴PF2⊥PF1,
∵PF1+PF2=2a
∴PF1=-PF2+2a=-b+2a
在Rt△PF1F′中,PF12+PF22=F1F22
即b=
| 2 |
| 3 |
∴c=
| a2-b2 |
| ||
| 3 |
∴离心率e=
| c |
| a |
| ||
| 3 |
故选:B.
点评:本小题主要考查椭圆的简单性质、圆的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,在圆锥曲线中,求离心率关键就是求三参数a,b,c的关系,属于基础题.

练习册系列答案
相关题目
由线y=x2在P处的切线的斜率为3,则P点的坐标为( )
A、(-
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
已知cos(75°+α)=
,则cos(30°-2α)的值为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若集合{1,a,
}={0,a2,a+b},则a2014+b2013的值为( )
| b |
| a |
| A、0 | B、1 | C、-1 | D、±1 |
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则
=( )
| b2 |
| a1+a2 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
 已知半椭圆
已知半椭圆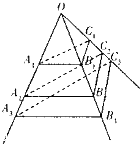 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=