题目内容
正六边形ABCDEF,且
=
,
=
,下列向量可表示为-
+
的是( )
| AC |
| a |
| BD |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据向量的加减的几何意义,首先求出得
=
-
,
=
+
,然后再加以计算判断即可.
| AB |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| BC |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
解答:
解:如图:
=
+
=
,①
=
-
=2
-
=
,②
由①②解得
=
-
,
=
+
,
∴
=-
=-
+
,
=2
=
+
,
=-
=-
-
,
=
-
=-
+
,
故选:A

| AC |
| AB |
| BC |
| a |
| BD |
| AD |
| AB |
| BC |
| AB |
| b |
由①②解得
| AB |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| BC |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
∴
| DE |
| AB |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| AD |
| BC |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
| EF |
| BC |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| CD |
| AD |
| AC |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
故选:A

点评:本题考查了平面向量加减的几何意义,以及正六边形的知识.注意平面向量是有方向性的,注意数形结合思想的应用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立.类比上述性质,在等比数列{bn}中,若b11=1,则有( )
| A、b1•b2•…•bn=b1•b2•…•b19-n |
| B、b1•b2•…•bn=b1•b2•…•b21-n |
| C、b1+b2+…+bn=b1+b2+…+b19-n |
| D、b1+b2+…+bn=b1+b2+…+b21-n |
设x,y为正实数,且满足x≤2,y≤3,x+y=3,则4x3+y3的最大值是( )
| A、24 | B、27 | C、33 | D、45 |
在△ABC中,若sin2A=sin2B+sin2C,则△ABC的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
已知
=(2,1),
=(x,1),且
+
与2
-
平行,则x等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、10 | B、-10 | C、2 | D、-2 |
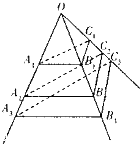 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=