题目内容
已知{
,
,
}是单位正交基底,
=-3
+4
-
,
-
=-8
+16
-3
,那么
•
= .
| i |
| j |
| k |
| a |
| i |
| j |
| k |
| a |
| b |
| i |
| j |
| k |
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:根据题意可得
=(-3,4,-1),
-
=(-8,16,-3),从而算出
=(5,-12,2).再利用向量数量积的坐标运算公式,即算出
•
的值.
| a |
| a |
| b |
| b |
| a |
| b |
解答:
解:∵{
,
,
}是单位正交基底,
∴
=-3
+4
-
=(-3,4,-1),
-
=-8
+16
-3
=(-8,16,-3)
由此可得
=
-(
-
)=(-3,4,-1)-(-8,16,-3)=(5,-12,2).
∴
•
=-3×5+4×(-12)+(-1)×2=-65.
故答案为:-65
| i |
| j |
| k |
∴
| a |
| i |
| j |
| k |
| a |
| b |
| i |
| j |
| k |
由此可得
| b |
| a |
| a |
| b |
∴
| a |
| b |
故答案为:-65
点评:本题给出向量在单位正交基底下的坐标,求它们的数量积.着重考查了单位向量、正交基底和向量数量积的坐标运算公式等知识,属于基础题.

练习册系列答案
相关题目
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| n(n+2) |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
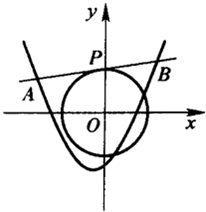 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;