Question

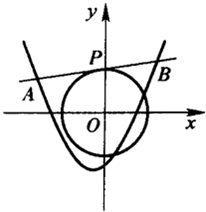设点P（m，n）在圆x²+y²=2上，l是过点P的圆的切线，切线l与函数y=x²+x+k（k∈R）的图象交于AB两点，点O是坐标原点，且△OAB是以AB为底的等腰三角形；
（1）试求出P纵坐标n足的等量关系；
（2）若将（1）中的等量关系右边化为零，左边关于n代数式可表为（n+1）²（ax²+bx+c）的形式，且满足条件的等腰三角形有有3个，求k的取值范围．

Answer 1

考点：圆方程的综合应用

专题：

分析：①写出过P的切线，然后分别设出A，B两个点的坐标．根据是已知题意列出3个等式，然后解出结果..通过P点纵坐标为n，代入P中求出n的等量关系．
②按照①的结果，通过把等量关系右边化为零，左边关于n的代数式表示为（n+1）²（ax²+bx+c）的形式，化简．然后根据满足条件的等腰三角形有3个，分别判断△＞0是否成立．经过计算分别求出K的取值范围即可．

解答： 解：（1）△OAB是以AB为底的等腰三角形，∴P是AB的中点．
过P点的切线：mx+ny=2．
设A（x₁，y₁），B（x₂，y₂），则y₁=x₁²+x₁+k①，y₂=x₂²+x₂+k②，x₁+x₂=2m．
②-①：y₂-y₁=（x₂+x₁）（x₂-x₁）+x₂-x₁，
∴

y2-y1

x2-x1

=x₁+x₂+1=2m+1，
∴-

m

n

=2m+1，
∴m=

-n

2n+1

，
（2）∵m²+n²=2，
∴（

-n

2n+1

）²+n²=2，
∴4n⁴+4n³-6n²-8n-2=0
即2n⁴+2n³-3n²-4n-1=0．
由已知，2n⁴+2n³-3n²-4n-1
=（n+1）²（an²+bn+c）=（n²+2n+1）（an²+bn+c）
=an⁴+（b+2a）n³+（c+a+2b）n²+（2c+b）n+c，
∴

a=2 b+2a=2 c+a+2b=-3 2c+b=-4 c=-1

，
∴a=2，b=-2，c=-1，
由2n⁴+2n³-3n²-4n-1=（n+1）²（2n²-2n-1）=0
∴n+1=0或2n²-2n-1=0，
∴n=-1或n=

1± 3

2

，
∴

m=-1 n=-1

或

m= 1- 3 2 n= 1+ 3 2

或

m= 1- 3 2 n= 1+ 3 2

，
由

mx+ny=2 y=x2+x+k

得nx²+（m+n）x+nk-2=0
当

m=-1 n=-1

时，x²+2x+k+2=0，△=4-4k-8＞0，k＜-1；
当

m= 1- 3 2 n= 1+ 3 2

时，

1+ 3

2

x²+x+

1+ 3

2

k-2=0，由△=1-4•

1+ 3

2

•（

1+ 3

2

k-2）＞0可得k＜

( 3 +7)( 3 -1)

4

；
当

m= 1- 3 2 n= 1+ 3 2

时，

1- 3

2

x²+x+

1- 3

2

k-2=0，由△=1-4•

1- 3

2

•（

1- 3

2

k-2）＞0可得k＜-1-

3 3

2

，
等腰三角形恰有3个等价于以上三个解都满足△＞0，
故k＜-1-

3 3

2

．

点评：本题考查直线与圆的关系的应用，通过直线与圆相切，对关系式进行分析，属于难题．