题目内容
设二次函数f(x)=ax2+bx+c满足一下条件
①x∈R时,f(x-4)=f(2-x),且f(x)≥x;
②x∈(0,2)时,f(x)≤(x+12)2;
③f(x)在R上的最小值0;
(1)求f(x)的解析式;
(2)求最大的实数m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x..
①x∈R时,f(x-4)=f(2-x),且f(x)≥x;
②x∈(0,2)时,f(x)≤(x+12)2;
③f(x)在R上的最小值0;
(1)求f(x)的解析式;
(2)求最大的实数m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x..
考点:函数恒成立问题,函数解析式的求解及常用方法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由已知求得函数的对称轴方程,再由x∈(0,2)时,x≤f(x)≤
(x2+1)恒成立求得f(1)=1,
结合函数的最小值联立方程组求得a,b,c的值,则函数解析式可求;
(2)由f(x+t)≤x在x∈[1,m]恒成立得到
在[1,m]上恒成立,分别求出两个函数的最大最小值,进一步得-(
-1)2≥-4,由此求得m的最大值.
| 1 |
| 2 |
结合函数的最小值联立方程组求得a,b,c的值,则函数解析式可求;
(2)由f(x+t)≤x在x∈[1,m]恒成立得到
|
| m |
解答:
解:(1)∵f(x-4)=f(2-x),
∴函数图象关于直线x=-1对称,
∴-
=-1,b=2a,
又∵x∈(0,2)时,x≤f(x)≤
(x2+1)恒成立,
∴1≤f(1)≤
(12+1)=1,即f(1)=1
∴a+b+c=1,
又∵f(x)在R上的最小值为0,
∴f(-1)=0,即a-b+c=0,
由
,解得a=c=
,b=
,
∴f(x)=
x2+
x+
;
(2)由(1)知f(x)=
x2+
x+
=
(x+1)2,
由f(x+t)≤x,得(x+t+1)2≤4x且x∈[1,m],
则
在[1,m]上恒成立,
∴
,
∵y=-x-2
-1在[1,m]上递减,
∴(-x-2
-1)max=-4,
∵y=-x+2
-1在[1,m]上递减,
∴(-x-2
-1)min=-m+2
-1=-(
-1)2,
∴-4≤t≤-(
-1)2,
∴-(
-1)2≥-4,
(
-1)2≤4,
∵m>1,
∴
-1≤2,
∴m≤9.
∴函数图象关于直线x=-1对称,
∴-
| b |
| 2a |
又∵x∈(0,2)时,x≤f(x)≤
| 1 |
| 2 |
∴1≤f(1)≤
| 1 |
| 2 |
∴a+b+c=1,
又∵f(x)在R上的最小值为0,
∴f(-1)=0,即a-b+c=0,
由
|
| 1 |
| 4 |
| 1 |
| 2 |
∴f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1)知f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
由f(x+t)≤x,得(x+t+1)2≤4x且x∈[1,m],
则
|
∴
|
∵y=-x-2
| x |
∴(-x-2
| x |
∵y=-x+2
| x |
∴(-x-2
| x |
| m |
| m |
∴-4≤t≤-(
| m |
∴-(
| m |
(
| m |
∵m>1,
∴
| m |
∴m≤9.
点评:本题考查了函数解析式的求解及常用方法,训练了利用恒成立求参数的取值范围,体现了数学转化思想方法,考查了学生灵活处理问题和解决问题的能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
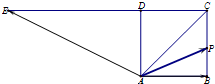 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,