题目内容
为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m3的部分,每立方米收费1.5元,并加收0.4元的城市污水处理费,请你写出某户居民每月应交纳的水费y(元)与用水量x(m3)之间的函数关系,然后设计一个求该函数值的程序框图,并写出程序语言.
考点:函数模型的选择与应用
专题:函数的性质及应用,算法和程序框图
分析:(1)设某户每月用水量为x(立方米),应交水费为y(元)由已知可得:该函数是分段函数,当x取不同范围内的值时,函数解析式不同,因此当给出一个自变量x的值时,必须先判断x 的范围,然后确定利用哪一段的解析式求函数值,由此求出算法.
(2)根据算法,画出程序框图及相应的程序语言.
(2)根据算法,画出程序框图及相应的程序语言.
解答:
解:(1)未超出7立方米时: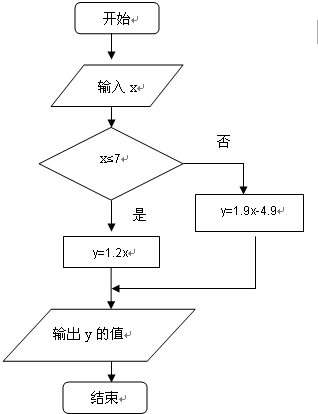
y=x×(1+0.2)=1.2x;
超出7立方米时:
y=7×1.2+(x-7)×(1.5+0.4)=1.9x-4.9,
∴y=
.
(2)该函数是分段函数,当x取不同范围内的值时,
函数解析式不同,
因此当给出一个自变量x的值时,
必须先判断x 的范围,
然后确定利用哪一段的解析式求函数值,
算法如下:
第一步,输入x;
第二步,如果x≤7,那么y=1.2x,
否则如果x>7,那么y=1.9x-4.9.
程序框图如图所示:

y=x×(1+0.2)=1.2x;
超出7立方米时:
y=7×1.2+(x-7)×(1.5+0.4)=1.9x-4.9,
∴y=
|
(2)该函数是分段函数,当x取不同范围内的值时,
函数解析式不同,
因此当给出一个自变量x的值时,
必须先判断x 的范围,
然后确定利用哪一段的解析式求函数值,
算法如下:
第一步,输入x;
第二步,如果x≤7,那么y=1.2x,
否则如果x>7,那么y=1.9x-4.9.
程序框图如图所示:
点评:本题考查的知识点是设计程序框图实际问题,编写程序解决分段函数问题,要分如下几个步骤:①对题目的所给的条件的分类进行总结,写出分段函数的解析式;②根据分类标准,设置判断框的个数及判断框中的条件;③分析函数各段的解析式,确定判断框的“是”与“否”分支对应的操作;④画出流程图,再编写满足题意的程序.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合 A={1,2},集合B满足A∪B=A,则集合B有( )
| A、1 | B、2 | C、3 | D、4 |
设点M(m,0)在椭圆
+
=1的长轴上,点p是椭圆上任意一点. 当
的模最小时,点p恰好落在椭圆的右顶点,则实数m的取值范围( )
| x2 |
| 16 |
| y2 |
| 12 |
| MP |
| A、[0,4] |
| B、[1,4] |
| C、[1,5] |
| D、[3,4] |
 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.