题目内容
 要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有
要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有考点:排列、组合及简单计数问题
专题:排列组合
分析:区域1可取4种颜色任何一种色,有
种,区域2只能取除区域1以外的颜色有
种,区域4与区域2不相邻,有
种;再对区域5与区域3分类讨论,最后利用乘法原理与加法原理运算即可求得答案.
| A | 1 4 |
| A | 1 3 |
| A | 1 3 |
解答:
解:首先,区域1可取4种颜色任何一种色,有
种,区域2只能取除1以外的颜色有
种;
区域4与区域2不相邻,也可取除1以外的3种颜色,有
种;
区域5有两种可能:①区域2,区域4取同一色,有
种;②区域2,区域4取不同色,区域5只有一色可取,有
种方法;
区域3也有2种可能:若区域2,区域4取同一色,有
种取法;若区域2,区域4取不同色,区域5只有一色可取,有
种方法;
区域2、区域4共
×
=3×3=9取法中,3种取法是同一色的,6种取法是不同色的;
所以,共有着色方法
×3×
×
+
×6×
×
=4×3×2×2+4×6×1×1
=48+24
=72种.
故答案为:72.
| A | 1 4 |
| A | 1 3 |
区域4与区域2不相邻,也可取除1以外的3种颜色,有
| A | 1 3 |
区域5有两种可能:①区域2,区域4取同一色,有
| A | 1 2 |
| A | 1 1 |
区域3也有2种可能:若区域2,区域4取同一色,有
| A | 1 2 |
| A | 1 1 |
区域2、区域4共
| A | 1 3 |
| A | 1 3 |
所以,共有着色方法
| A | 1 4 |
| A | 1 2 |
| A | 1 2 |
| A | 1 4 |
| A | 1 1 |
| A | 1 1 |
=4×3×2×2+4×6×1×1
=48+24
=72种.
故答案为:72.
点评:本题考查排列、组合及简单计数问题,考查分类讨论思想与分析、运算及求解能力,属于中档题.

练习册系列答案
相关题目
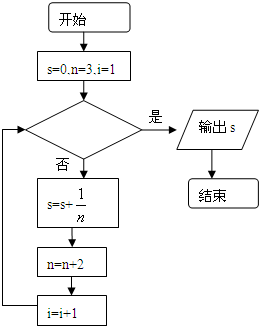
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 21 |

| A、i>10? |
| B、i<10? |
| C、i>20? |
| D、i<20? |
已知f(x)=ax3+bx-4,若f(-2)=2,则f(2)=( )
| A、-2 | B、-4 | C、-6 | D、-10 |