题目内容
在不等式组
对应的平面区域内任取一点(a,b),则关于x的方程x2+2ax+b2=0有实根的概率是 .
|
考点:几何概型
专题:概率与统计
分析:首先分析一元二次方程有实根的条件,得到a2≥b2.本题是一个几何概型,试验的全部结束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},满足条件的构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b},根据概率等于面积之比,得到概率.
解答:
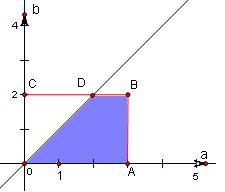 解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.
解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.
设点M的坐标为(a,b),由于a∈[0,3],b∈[0,2],所以,所有的点M对构成坐标平面上一个区域(如图中的矩形OABC),即所有的基本事件构成坐标平面上的区域OABC,其面积为2×3=6.
由于a在[0,3]上随机抽取,b在[0,2]上随机抽取,
所以,组成区域OABC的所有基本事件是等可能性的.
又由于满足条件0≤a≤3,且0≤b≤2,且a2≥b2,即a≥b的平面区域如图中阴影部分所示,其面积为
×(1+3)×2=4,
所以,事件A组成平面区域的面积为4,所以P(A)=
=
.
所以,方程x2+2ax+b2=0有实根的概率为
.
故答案为:
 解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.
解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.设点M的坐标为(a,b),由于a∈[0,3],b∈[0,2],所以,所有的点M对构成坐标平面上一个区域(如图中的矩形OABC),即所有的基本事件构成坐标平面上的区域OABC,其面积为2×3=6.
由于a在[0,3]上随机抽取,b在[0,2]上随机抽取,
所以,组成区域OABC的所有基本事件是等可能性的.
又由于满足条件0≤a≤3,且0≤b≤2,且a2≥b2,即a≥b的平面区域如图中阴影部分所示,其面积为
| 1 |
| 2 |
所以,事件A组成平面区域的面积为4,所以P(A)=
| 4 |
| 6 |
| 2 |
| 3 |
所以,方程x2+2ax+b2=0有实根的概率为
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
设全集U={a,b,c,d},A={a,c},B={b},则(∁UB)∩A=( )
| A、∅ | B、{a,c} |
| C、{a} | D、{c} |
已知U=R,M={x|x2-4x+4>0},则∁UM=( )
| A、R | B、∅ | C、{2} | D、{0} |
已知实数x>0,y>0,0<λ<2,且x+y=3,则
+
+
的最小值为( )
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
方程x=2+log
x的根所在的区间是( )
| 1 |
| 2 |
| A、(1,2) |
| B、(0,1) |
| C、(2,3) |
| D、(4,5) |
 要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有
要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有 如图,在一段线路中并联着3个自动控制的开关,只要其中有一个开关能够闭合,线路就正常工作,假在某段时间内每个开关能够闭合的概率是0.5,请你用树状图求出在这段时间内正常工作的概率.
如图,在一段线路中并联着3个自动控制的开关,只要其中有一个开关能够闭合,线路就正常工作,假在某段时间内每个开关能够闭合的概率是0.5,请你用树状图求出在这段时间内正常工作的概率.