题目内容
已知某商品的进货单价为1元/件，商户甲往年以单价2元/件销售该商品时，年销量为1万件，今年拟下调销售单价以提高销量，增加收益．据测算，若今年的实际销售单价为x元/件（1≤x≤2），今年新增的年销量（单位：万件）与（2-x）2成正比，比例系数为4．
（1）写出今年商户甲的收益y（单位：万元）与今年的实际销售单价x间的函数关系式；
（2）商户甲今年采取降低单价，提高销量的营销策略是否能获得比往年更大的收益（即比往年收益更多）？说明理由．
（1）写出今年商户甲的收益y（单位：万元）与今年的实际销售单价x间的函数关系式；
（2）商户甲今年采取降低单价，提高销量的营销策略是否能获得比往年更大的收益（即比往年收益更多）？说明理由．
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：（1）直接根据题意可写出今年的销售量，从而可计算出客户甲的收益；
（2）根据（1）中建立的函数，求导，令导数等于0，求出极大值点和极大值，再求出x=2时的函数值，进行比较，最大的就是最大值．
（2）根据（1）中建立的函数，求导，令导数等于0，求出极大值点和极大值，再求出x=2时的函数值，进行比较，最大的就是最大值．
解答：
解 （1）由题意知，今年的年销售量为1+4（x-2）2（万件）．
∵每销售一件，商户甲可获利（x-1）元，
∴今年商户甲的收益
y=[1+4（x-2）2]（x-1）
=4x3-20x2+33x-17，（1≤x≤2）．
（2）由（1）知
y=4x3-20x2+33x-17，1≤x≤2，
∴y′=12x2-40x+33=（2x-3）（6x-11）．
令y′=0，解得x=
，或x=
．列表如下：
又f（
）=1，f（2）=1，
∴f（x）在区间[1，2]上的最大值为1（万元）．
∵往年的收益为（2-1）×1=1（万元），
∴商户甲采取降低单价，提高销量的营销策略不能获得比往年更大的收益．
∵每销售一件，商户甲可获利（x-1）元，
∴今年商户甲的收益
y=[1+4（x-2）2]（x-1）
=4x3-20x2+33x-17，（1≤x≤2）．
（2）由（1）知
y=4x3-20x2+33x-17，1≤x≤2，
∴y′=12x2-40x+33=（2x-3）（6x-11）．
令y′=0，解得x=
| 3 |
| 2 |
| 11 |
| 6 |
| x | （1，
|
|
（
|
|
（
| ||||||||||||
| f′（x） | + | 0 | - | 0 | + | ||||||||||||
| f（x） | 递增 | 极大值 | 递减 | 极小值 | 递增 |
| 3 |
| 2 |
∴f（x）在区间[1，2]上的最大值为1（万元）．
∵往年的收益为（2-1）×1=1（万元），
∴商户甲采取降低单价，提高销量的营销策略不能获得比往年更大的收益．
点评：本题主要考查实际问题中的数据提取和分析能力，考查导数再求函数最大值中的应用，属于中档题．
练习册系列答案
相关题目
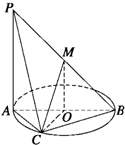如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：
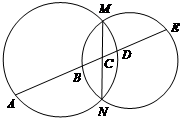如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB•CD=BC•DE．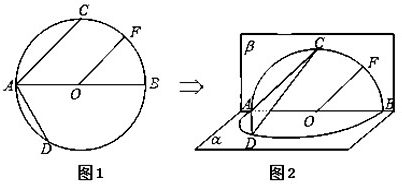
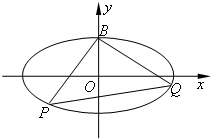已知椭圆C：
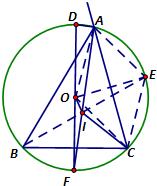如图，设O，I分别为△ABC的外心、内心，且∠B=60°，AB＞BC，∠A的外角平分线交⊙O于D，已知AD=18，则OI=．