题目内容
下列命题:
①“若ma2>na2,则m>n”的逆否命题;
②“若A与B是互斥事件,则A与B是对立事件”的逆命题;
③“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题;
④“若|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),则2b<a”的逆否命题.
其中是假命题个数有( )
①“若ma2>na2,则m>n”的逆否命题;
②“若A与B是互斥事件,则A与B是对立事件”的逆命题;
③“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题;
④“若|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),则2b<a”的逆否命题.
其中是假命题个数有( )
| A、0 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:等差数列与等比数列,不等式的解法及应用,简易逻辑
分析:①判定命题“若ma2>na2,则m>n”的真假性,得到它的逆否命题的真假性;
②写出“若A与B是互斥事件,则A与B是对立事件”的逆命题,再判定逆命题的真假性;
③写出“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题,通过举例说明它的真假性;
④判定命题|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),则2b<a的真假性,得到它的逆否命题的真假性.
②写出“若A与B是互斥事件,则A与B是对立事件”的逆命题,再判定逆命题的真假性;
③写出“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题,通过举例说明它的真假性;
④判定命题|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),则2b<a的真假性,得到它的逆否命题的真假性.
解答:
解:①∵ma2>na2,∴a2>0,∴m>n,
∴命题“若ma2>na2,则m>n”是真命题,它的逆否命题也是真命题;
②“若A与B是互斥事件,则A与B是对立事件”的逆命题是:
“若A与B是对立事件,则A与B是互斥事件”,它是真命题;
因为对立事件是互斥事件,互斥事件不一定是对立事件;
③“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题是:
“在等差数列{an}中,若m+k≠p+h,则am+ak≠ap+ah”,若{an}是常数列时,命题不正确;
∴命题③是假命题;
④∵|2x+2|<a,∴|x+1|<
,
又|x+1|<b,(a>0,b>0),
∵|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),
∴b<
,即2b<a是真命题;
∴它的逆否命题也是真命题;
综上,以上命题中假命题的个数是1;
故选:D.
∴命题“若ma2>na2,则m>n”是真命题,它的逆否命题也是真命题;
②“若A与B是互斥事件,则A与B是对立事件”的逆命题是:
“若A与B是对立事件,则A与B是互斥事件”,它是真命题;
因为对立事件是互斥事件,互斥事件不一定是对立事件;
③“在等差数列{an}中,若m+k=p+h,则am+ak=ap+ah”的否命题是:
“在等差数列{an}中,若m+k≠p+h,则am+ak≠ap+ah”,若{an}是常数列时,命题不正确;
∴命题③是假命题;
④∵|2x+2|<a,∴|x+1|<
| a |
| 2 |
又|x+1|<b,(a>0,b>0),
∵|2x+2|<a的必要不充分条件是|x+1|<b(a>0,b>0),
∴b<
| a |
| 2 |
∴它的逆否命题也是真命题;
综上,以上命题中假命题的个数是1;
故选:D.
点评:本题通过判定命题的真假考查了四种命题之间的关系以及不等式、对立与互斥事件、等差数列和充分、必要条件的知识,是综合性题目.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
设实数x,y满足不等式组
,则
的取值范围是( )
|
| y |
| x+3 |
A、[0,
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
设全集U={1,2,3,4,5,6},M={1,2,3},N={3,4,5},则(∁UM)∩N=( )
| A、{3} |
| B、{4,5} |
| C、{3,4,5} |
| D、(4,5) |

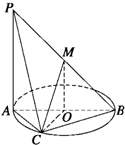 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题: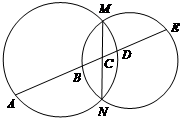 如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB•CD=BC•DE.
如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB•CD=BC•DE.