题目内容
2.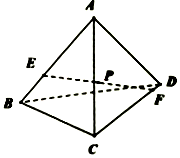 如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)
如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)
分析 由题意画出图形,通过取特殊点找到P的轨迹,再由圆的面积公式得答案.
解答 解:如图,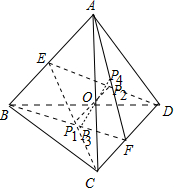
当E为AB中点时,F分别在C,D处,满足|EF|=$\sqrt{3}$,
此时EF的中点P在EC,ED的中点P1,P2的位置上,
当F为CD中点时,E分别在A,B处,满足|EF|=$\sqrt{3}$,
此时EF的中点P在BF,AF的中点P3,P4的位置上,
连接P1P2,P3P4相交于点O,则四点P1,P2,P3,P4共圆,
圆心为O,圆的半径为$\frac{1}{2}$,则EF中点P的轨迹为L为以O为圆心,以$\frac{1}{2}$为半径的圆,
其测度|L|=$2π×\frac{1}{2}=π$.
故答案为:π.
点评 本题考查空间中的线面关系,考查数形结合的解题思想方法,明确P的轨迹是关键,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
14.已知函数$f(x)=\sqrt{3}sin2x-cos2x$的图象在区间$[{0,\frac{a}{3}}]$和$[{2a,\frac{4π}{3}}]$上均单调递增,则正数a的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{12}}]$ | B. | $[{\frac{5π}{12},π}]$ | C. | $[{\frac{π}{4},π}]$ | D. | $[{\frac{π}{4},\frac{2π}{3}}]$ |
11.已知集合M={x|1<x≤3},若N={x|2<x≤5},则M∪N=( )
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
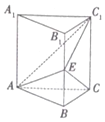 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.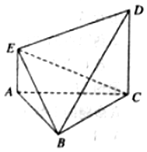 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.