题目内容
7.已知函数f(x)=ax+x2-xlna-b(a>1,b∈R),e是自然对数的底数.若存在x1,x2∈[-1,1],使得|f(x1)-f(x2|≥e-1,则实数a的取值范围是[e,+∞).(参考公式:(ax)′=axlna)分析 存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,等价于当x∈[-1,1]时,|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1,利用导数易求函数f(x)在[-1,1]上的最小值f(0),而f(x)max=max{f(-1),f(1)},作差后构造函数可得f(x)max=f(1),从而有f(1)-f(0)≥e-1,再构造函数利用单调性可求得a的范围.
解答 解:f(x)=ax+x2-xlna-b,∵存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,
∴当x∈[-1,1]时,|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1.
f'(x)=axlna+2x-lna=2x+(ax-1)lna,
①当x>0时,由a>1,可知ax-1>0,lna>0,∴f'(x)>0;
②当x<0时,由a>1,可知ax-1<0,lna>0,∴f'(x)<0;
③当x=0时,f'(x)=0,∴f(x)在[-1,0]上递减,在[0,1]上递增.
∴当x∈[-1,1]时,f(x)min=f(0)=1-b,f(x)max=max{f(-1),f(1)},
而f(1)-f(-1)=(a+1-lna-b)-($\frac{1}{a}$+1+lna-b)=a-$\frac{1}{a}$-2lna.
设g(t)=t-$\frac{1}{t}$-2lnt(t>0),∵g′(t)=1+$\frac{1}{{t}^{2}}$-$\frac{2}{t}$=($\frac{1}{t}$-1)2≥0(当t=1时取等号),
∴g(t)=t-$\frac{1}{t}$-2lnt在t∈(0,+∞)上单调递增,而g(1)=0,
∴当t>1时,g(t)>0,∴当a>1时,a-$\frac{1}{a}$-2lna>0,
∴f(1)>f(-1).
∴f(1)-f(0)≥e-1,∴a-lna≥e-1,即a-lna≥e-lne.
设h(a)=a-lna(a>1),则h′(a)=1-$\frac{1}{a}$=$\frac{a-1}{a}$>0,
∴函数h(a)=a-lna(a>1)在(1,+∞)上为增函数,∴a≥e,
∴a的取值范围是[e,+∞).
故答案为:[e,+∞).
点评 本题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、不等式问题,考查考生综合运用数学知识解决问题的能力,同时也考查函数与方程思想、化归与转化思想,是中档题.

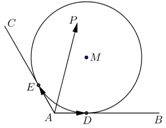 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )| A. | $[1,4+2\sqrt{3}]$ | B. | $[4-2\sqrt{3},4+2\sqrt{3}]$ | C. | $[1,2+\sqrt{3}]$ | D. | $[2-\sqrt{3},2+\sqrt{3}]$ |
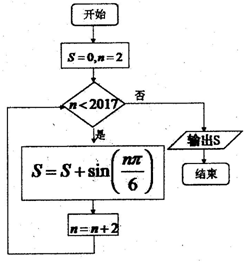
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
附:(若随机变量ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%,P(μ-3σ<ξ<μ+3σ)=99.72%)
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
| A. | {1,2} | B. | {0,1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
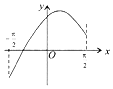
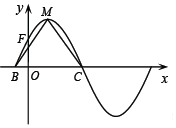 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.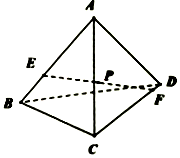 如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)
如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)