题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若|
|=|
|,则双曲线的离心率( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OF |
| OP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设双曲线
-
=1(a>0,b>0)的左焦点为F,连结PF′,OE,由已知条件,利用双曲线的性质,推导出|PF|a,|PF|=3a,PF⊥PF′,由此能求出双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:设双曲线
-
=1(a>0,b>0)的左焦点为F,右焦点为F′,
连结PF′,OE,
∵过左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,
∴OE⊥PF,
又∵|OF|=|OP|,∴E为PF的中点,∴OE∥PF′,
∴|PF|=2|OE|=2×
=a,
由双曲线定义知|PF|-|PF′|=2a,
∴|PF|=|PF′|+2a=3a,
∵OE∥PF′,∴PF⊥PF′,
在Rt△PFF′中,(3a)2+a2=(2c)2,
解得c=
a,
∴e=
=
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
连结PF′,OE,
∵过左焦点F(-c,0)(c>0)作圆x2+y2=
| a2 |
| 4 |

∴OE⊥PF,
又∵|OF|=|OP|,∴E为PF的中点,∴OE∥PF′,
∴|PF|=2|OE|=2×
| a |
| 2 |
由双曲线定义知|PF|-|PF′|=2a,
∴|PF|=|PF′|+2a=3a,
∵OE∥PF′,∴PF⊥PF′,
在Rt△PFF′中,(3a)2+a2=(2c)2,
解得c=
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故选:A.
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的简单性质.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图,在半径为R的圆C中,已知弦AB的长为5,则
•
=( )
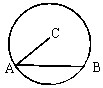
| AB |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线的离心率为3,且它有一个焦点与抛物线y2=12x的焦点相同,那么双曲线的渐近线方程为( )
| A、x±2y=0 | ||
| B、2x±y=0 | ||
C、2
| ||
D、x±2
|
下列说法错误的是( )
| A、用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 |
| B、有两个面平行,其余各个面都是梯形的几何体一定都是棱台 |
| C、圆锥的轴截面是等腰三角形 |
| D、用一个平面去截球,截面是圆 |