题目内容
设函数f（x）=
的定义域为A，函数g（x）=
的定义域为B，求A∩B，A∪B，∁RB．
| -x2-4x+5 |
| ||
| x-1 |
考点：交、并、补集的混合运算
专题：集合
分析：求出f（x）与g（x）的定义域确定出A与B，找出A与B的交集，并集，求出B的补集即可．
解答：
解：由f（x）=
，得到-x2-4x+5≥0，即x2+4x-5≤0，
解得：-5≤x≤1，即A=[-5，1]，
由g（x）=
，得到4-x2≥0，且x-1≠0，
解得：-2≤x≤2，且x≠1，即B=[-2，1）∪（1，2]，
则A∩B=[-2，1），A∪B=[-5，2]，∁RB=（-∞，-2）∪（2，+∞）∪{1}．
| -x2-4x+5 |
解得：-5≤x≤1，即A=[-5，1]，
由g（x）=
| ||
| x-1 |
解得：-2≤x≤2，且x≠1，即B=[-2，1）∪（1，2]，
则A∩B=[-2，1），A∪B=[-5，2]，∁RB=（-∞，-2）∪（2，+∞）∪{1}．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
不等式3-|-2x-1|＞0的解集是：（ ）
| A、{x|x＜-2或x＞1} |
| B、{x|-2＜x＜1} |
| C、{x|-1＜x＜2} |
| D、R |
（5
）0.5+（-1）-1÷0.75-2+（2
） -
=（ ）
| 1 |
| 16 |
| 10 |
| 27 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
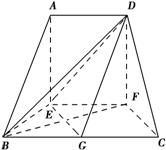在如图的多面体中，AE⊥底面BEFC，AD∥EF∥BC，BE=AD=EF=