题目内容
命题“?x∈（0，+∞），2x＞1”的否定是（ ）
| A、?x0∉（0，+∞），2x0≤1 |
| B、?x0∈（0，+∞），2x0≤1 |
| C、?x∉（0，+∞），2x≤1 |
| D、?x∈（0，+∞），2x＜1 |
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，
所以命题“?x∈（0，+∞），2x＞1”的否定是：?x0∈（0，+∞），2x0≤1．
故选：B．
所以命题“?x∈（0，+∞），2x＞1”的否定是：?x0∈（0，+∞），2x0≤1．
故选：B．
点评：本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列命题：
①幂函数的图象都经过点（1，1）和点（0，0）；
②幂函数的图象不可能是一条直线；
③n=0时，函数y=xn的图象是一条直线；
④幂函数y=xn，当n＞0时是增函数；
⑤幂函数y=xn，当n＜0时，在第一象限内函数值随x值的增大而减小．
⑥幂函数的图象不可能在第四象限；
其中正确的是（ ）
①幂函数的图象都经过点（1，1）和点（0，0）；
②幂函数的图象不可能是一条直线；
③n=0时，函数y=xn的图象是一条直线；
④幂函数y=xn，当n＞0时是增函数；
⑤幂函数y=xn，当n＜0时，在第一象限内函数值随x值的增大而减小．
⑥幂函数的图象不可能在第四象限；
其中正确的是（ ）
| A、③⑤⑥ | B、⑤⑥ |
| C、②③⑥ | D、①②③④ |
使（3-2x-x2） -
有意义的x的取值范围是（ ）
| 3 |
| 4 |
| A、R |
| B、x≠1且x≠3 |
| C、-3＜x＜1 |
| D、x＜-3或x＞1 |
在等差数列{an}中，若a4+a6+a8+a10+a12=90，则a10-
a14的值为（ ）
| 1 |
| 3 |
| A、12 | B、14 | C、16 | D、18 |
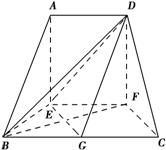在如图的多面体中，AE⊥底面BEFC，AD∥EF∥BC，BE=AD=EF=