题目内容
已知边长为2的正方体ABCD-A1B1C1D1,P是棱CC1上任一点,CC1=m,(0<m<2).
(1)是否存在满足条件的实数m,使平面BPD1⊥面BDD1B1?若存在,求出m的值;不存在,说明理由.
(2)是否存在实数m,使得三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等?存在,求出m的值;不存在,说明理由.
(1)是否存在满足条件的实数m,使平面BPD1⊥面BDD1B1?若存在,求出m的值;不存在,说明理由.
(2)是否存在实数m,使得三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等?存在,求出m的值;不存在,说明理由.
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)存在m=1,使平面BPD1⊥面BDD1B1,连接AC,AC1,BD1,设AC1∩BD1=H,由H是AC1的中点,连接PH,进而由线面垂直的判定定理和面面垂直的判定定理可得答案;
(2)存在m=
,使三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等,由三棱锥B-PAC即四棱锥P-ABC和四棱锥P-A1B1C1D1的底面积之比为1:2,三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等,可得:两个棱锥的高之比应为:2:1,即PC:PC1=2:1,即m:(2-m)=2:1,解得答案.
(2)存在m=
| 4 |
| 3 |
解答:
解:(1)存在m=1,使平面BPD1⊥面BDD1B1,理由如下:
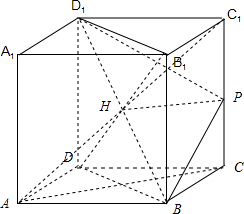
连接AC,AC1,BD1,设AC1∩BD1=H,
由H是AC1的中点,连接PH,
由m=1时,P为CC1的中点,可得PH是△C1AC的中位线,
则PH∥AC,
∵AC⊥BD,AC⊥BB1,BD∩BB1=B,BD,BB1?面BDD1B1,
∴AC⊥面BDD1B1,
∴PH⊥面BDD1B1,
又∵PH?平面BPD1,
∴平面BPD1⊥面BDD1B1;
(2)存在m=
,使三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等,理由如下:
∵三棱锥B-PAC即四棱锥P-ABC和四棱锥P-A1B1C1D1的底面积之比为1:2,
若三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等,
则两个棱锥的高之比应为:2:1,
即PC:PC1=2:1,
即m:(2-m)=2:1,
解得:m=

连接AC,AC1,BD1,设AC1∩BD1=H,
由H是AC1的中点,连接PH,
由m=1时,P为CC1的中点,可得PH是△C1AC的中位线,
则PH∥AC,
∵AC⊥BD,AC⊥BB1,BD∩BB1=B,BD,BB1?面BDD1B1,
∴AC⊥面BDD1B1,
∴PH⊥面BDD1B1,
又∵PH?平面BPD1,
∴平面BPD1⊥面BDD1B1;
(2)存在m=
| 4 |
| 3 |
∵三棱锥B-PAC即四棱锥P-ABC和四棱锥P-A1B1C1D1的底面积之比为1:2,
若三棱锥B-PAC和四棱锥P-A1B1C1D1的体积相等,
则两个棱锥的高之比应为:2:1,
即PC:PC1=2:1,
即m:(2-m)=2:1,
解得:m=
| 4 |
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面垂直的判定,棱锥的体积,难度中档.

练习册系列答案
相关题目
已知集合M={x|x≤1},P={x|x>t},若M∩P≠∅,则实数t应该满足的条件是( )
| A、t>1 | B、t≥1 |
| C、t<1 | D、t≤1 |
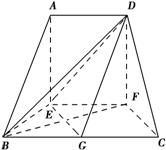 在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=
在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=