题目内容
已知函数f(x)=1-
(a>0且a≠1)是定义在R上的奇函数.
(1)求实数a及函数f(x)的值域;
(2)关于x的不等式t•f(x)≤2x+2对任意x∈R恒成立,求实数t的取值范围;
(3)附加题:当x、y>0时,求证f(
)≥
.
| 4 |
| 2ax+a |
(1)求实数a及函数f(x)的值域;
(2)关于x的不等式t•f(x)≤2x+2对任意x∈R恒成立,求实数t的取值范围;
(3)附加题:当x、y>0时,求证f(
| x+y |
| 2 |
| f(x)+f(y) |
| 2 |
考点:函数恒成立问题,函数的值域
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由定义在实数上的奇函数有f(0)=0列式求得a的值,并结合指数函数的值域求得函数f(x)的值域;
(2)由x得范围对x分类,然后利用分离参数法求得实数t的取值范围;
(3)要证明当x、y>0时,f(
)≥
,即证明函数f(x)为上凸增函数,借助于二次求导可得答案.
(2)由x得范围对x分类,然后利用分离参数法求得实数t的取值范围;
(3)要证明当x、y>0时,f(
| x+y |
| 2 |
| f(x)+f(y) |
| 2 |
解答:
(1)解:∵函数f(x)=1-
(a>0且a≠1)是定义在(-∞,+∞)上的奇函数,
∴f(0)=1-
=0,解得a=2,
∴f(x)=1-
=1-
.
∵2x+1>1,
∴0<
<1,-1<1-
<1,
则f(x)∈(-1,1);
(2)解:由(1)得f(x)=
,
关于x的不等式t•f(x)≤2x+2对任意x∈R恒成立,
当f(x)=0时,对于任意实数t都成立;
当f(x)∈(0,1),即x∈(0,+∞)时,
则等价于t≤
=
=
.
令m=2x-1,则m>0,
即t≤m+
+5.
∵m+
+5≥2
+5=2
+5(当且仅当m=
时取等号).
∴t≤2
+5;
当f(x)∈(-1,0),即x∈(-∞,0)时,
则等价于t≥
=
=
.
令m=2x-1,则-1<m<0,
即t≥m+
+5.
∵m+
+5<-2.
t≥-2.
综上,所求的t范围是:-2≤t≤2
+5;
(3)证明:由(1)得f(x)=
=1-
,
∵f′(x)=(1-
)′=
>0,
∴f(x)为(0,+∞)上的增函数,
又[f′(x)]′=
=
<0(x>1).
∴函数f(x)=
为上凸增函数,
则f(
)≥
.
| 4 |
| 2ax+a |
∴f(0)=1-
| 4 |
| 2+a |
∴f(x)=1-
| 4 |
| 2•2x+2 |
| 2 |
| 2x+1 |
∵2x+1>1,
∴0<
| 1 |
| 2x+1 |
| 2 |
| 2x+1 |
则f(x)∈(-1,1);
(2)解:由(1)得f(x)=
| 2x-1 |
| 2x+1 |
关于x的不等式t•f(x)≤2x+2对任意x∈R恒成立,
当f(x)=0时,对于任意实数t都成立;
当f(x)∈(0,1),即x∈(0,+∞)时,
则等价于t≤
| 2x+2 |
| f(x) |
| (2x+2)(2x+1) |
| 2x-1 |
| (2x-1+3)(2x-1+2) |
| 2x-1 |
令m=2x-1,则m>0,
即t≤m+
| 6 |
| m |
∵m+
| 6 |
| m |
m•
|
| 6 |
| 6 |
∴t≤2
| 6 |
当f(x)∈(-1,0),即x∈(-∞,0)时,
则等价于t≥
| 2x+2 |
| f(x) |
| (2x+2)(2x+1) |
| 2x-1 |
| (2x-1+3)(2x-1+2) |
| 2x-1 |
令m=2x-1,则-1<m<0,
即t≥m+
| 6 |
| m |
∵m+
| 6 |
| m |
t≥-2.
综上,所求的t范围是:-2≤t≤2
| 6 |
(3)证明:由(1)得f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
∵f′(x)=(1-
| 2 |
| 2x+1 |
| 2•2xln2 |
| (2x+1)2 |
∴f(x)为(0,+∞)上的增函数,
又[f′(x)]′=
| 2•ln22•2x(2x+1)2-4•ln22•22x(2x+1) |
| (2x+1)4 |
=
| 2ln22•2x(2x+1)(1-2x) |
| (2x+1)4 |
∴函数f(x)=
| 2x-1 |
| 2x+1 |
则f(
| x+y |
| 2 |
| f(x)+f(y) |
| 2 |
点评:本题考查函数的奇偶性,单调性,不等式恒成立含参数的取值范围.考查转化计算、推理论证,参数分离的方法与能力,考查了利用导数研究函数的单调性,是压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=(
)x-log5x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
| 1 |
| 5 |
| A、恒为正 | B、等于零 |
| C、恒为负 | D、不大于零 |
若f(x)=-x2+ax在区间[0,1]上是增函数,在区间[3,4]上是减函数,则实数a的取值范围是( )
| A、(0,3) |
| B、(1,3) |
| C、[1,3] |
| D、(0,4] |
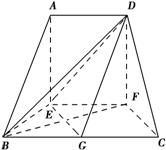 在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=
在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=