题目内容
请作出函数f（x）=xcosx2的图象，并说明具体步骤．
考点：函数的图象
专题：函数的性质及应用
分析：先分析函数的奇偶性，及极值点，描点连线后可得函数f（x）=xcosx2的图象．
解答：
解：分析函数的奇偶性，可得f（-x）=-xcos（-x）2=-xcosx2=-f（x）
故函数为奇函数，其图象关于原点对称，
分别令x2=kπ，k∈Z，描出对应的点，
可得函数f（x）=xcosx2的图象如下图所示：
故函数为奇函数，其图象关于原点对称，
分别令x2=kπ，k∈Z，描出对应的点，
可得函数f（x）=xcosx2的图象如下图所示：
点评：本题考查的知识点是函数的图象，其中非基本初等函数的图象要先分析其性质，进而描点画出草图．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
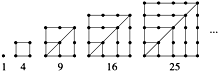我们把1，4，9，16，25，…这些数称做正方形数，这是因为这些数目的点子可以排成一个正方形（如图）．试求第n个正方形数是（ ）| A、n（n-1） |
| B、n（n+1） |
| C、n2 |
| D、（n+1）2 |