题目内容
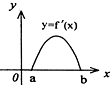设f′（x）是f（x）的导函数，f′（x）的图象如图所示，则f（x）的图象只可能是（ ）A、 |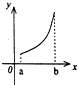
B、 |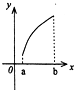
C、 |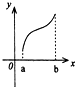
D、 |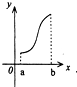
考点：函数的单调性与导数的关系
专题：导数的概念及应用
分析：由函数单调性和导数关系可得f（x）单调递增，且函数的增长先慢后快再变慢，结合选项可得答案．
解答：
解：由图可得f′（x）≥0，且导数值先小后大再变小，
对应f（x）单调递增，且函数的增长先慢后快再变慢，
结合选项可知选项D符合
故选：D
对应f（x）单调递增，且函数的增长先慢后快再变慢，
结合选项可知选项D符合
故选：D
点评：本题考查函数的单调性与导数的关系，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
若有一段演绎推理：“大前提：对任意实数a，都有（
）n=a．小前提：已知a=-2为实数．结论：（
）4=-2．”这个结论显然错误，是因为（ ）
| n | a |
| 4 | -2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
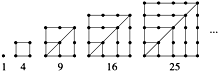我们把1，4，9，16，25，…这些数称做正方形数，这是因为这些数目的点子可以排成一个正方形（如图）．试求第n个正方形数是（ ）| A、n（n-1） |
| B、n（n+1） |
| C、n2 |
| D、（n+1）2 |
设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．则P（ξ=0）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（1+x）2n+1的展开式中，二项式系数最大的项所在的项数是（ ）
| A、n，n+1 |
| B、n-1，n |
| C、n+1，n+2 |
| D、n+2，n+3 |
设点A，B分别在直线3x-y+5=0和3x-y-13=0上运动，线段AB的中点M恒在圆x2+y2=8内，则点M的横坐标的取值范围为（ ）
A、（
| ||
B、（-2，-
| ||
C、（2，
| ||
D、（-
|