题目内容
设函数f(x)=2|x-3|+|x-4|.
(Ⅰ)求不等式f(x)<2的解集;
(Ⅱ)若不等式f(x)<ax的解集不是空集,求实数a的取值范围.
(Ⅰ)求不等式f(x)<2的解集;
(Ⅱ)若不等式f(x)<ax的解集不是空集,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)把要求的不等式转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)若不等式f(x)<ax的解集不是空集,则函数f(x)的图象有一部分在直线y=ax的下方,数形结合求得直线的斜率a的范围.
(Ⅱ)若不等式f(x)<ax的解集不是空集,则函数f(x)的图象有一部分在直线y=ax的下方,数形结合求得直线的斜率a的范围.
解答:
解:(Ⅰ)由不等式f(x)<2可得
①,或
②,
或
③.
解①求得
<x<3,解②求得3≤x<4,解③求得x∈∅,
综上可得,不等式的解集为(
,4).
(Ⅱ)∵f(x)=
,
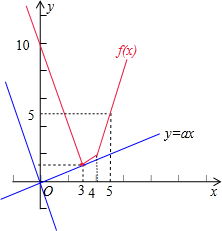
若不等式f(x)<ax的解集不是空集,则函数f(x)的图象有一部分在直线y=ax的下方,
如图所示:可得 a>
=
,或a<-3,求得a的范围为(
,+∞)∪(-∞,-3).
|
|
或
|
解①求得
| 8 |
| 3 |
综上可得,不等式的解集为(
| 8 |
| 3 |
(Ⅱ)∵f(x)=
|
若不等式f(x)<ax的解集不是空集,则函数f(x)的图象有一部分在直线y=ax的下方,
如图所示:可得 a>
| 1-0 |
| 3-0 |
| 1 |
| 3 |
| 1 |
| 3 |

点评:本题主要考查绝对值不等式的解法,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
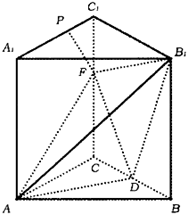 在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2.
在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2.