题目内容
给出下列三个函数的图象：
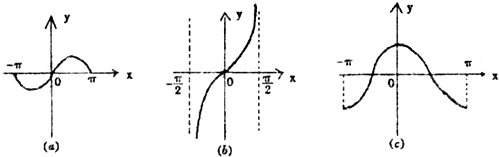
它们对应的函数表达式分别满足下列性质中的一条：
①f（2x）=2[f（x）]2-1
②f(x+y)=
③[f（2x）]2=4[f（x）]2（1-[f（x）]2）
则正确的对应方式是（ ）
它们对应的函数表达式分别满足下列性质中的一条：
①f（2x）=2[f（x）]2-1
②f(x+y)=
| f(x)+f(y) |
| 1-f(x)f(y) |
③[f（2x）]2=4[f（x）]2（1-[f（x）]2）
则正确的对应方式是（ ）
| A、（a）-①，（b）-②，（c）-③ |
| B、（b）-①，（c）-②，（a）-③ |
| C、（c）-①，（b）-②，（a）-③ |
| D、（a）-①，（c）-②，（b）-③ |
考点：函数的图象
专题：函数的性质及应用
分析：根据函数的图象的特点和对应的表达式的特点，即可判断得出．
解答：
解：由图象可知，（a）关于原点对称，（b）关于原点对称，图象越来越接近x=±
，但不是和x=±
相交，（c）图象关于y轴对称，．
∵cos2x=2cos2x-1，tan（x+y）=
，（sin2x）=4sin2x（1-sin2x），
∴（a）-③，（b）=②，（c）-①
故选：C．
| π |
| 2 |
| π |
| 2 |
∵cos2x=2cos2x-1，tan（x+y）=
| tanx+tany |
| 1-tanxtany |
∴（a）-③，（b）=②，（c）-①
故选：C．
点评：本题主考查了正弦函数，余弦函数，正切函数的图象，以及三角函数的二倍角公式，属于中档题．
练习册系列答案
相关题目
在△ABC中，A=60°，b=1，c=4，则△ABC外接圆的直径为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
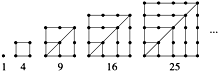我们把1，4，9，16，25，…这些数称做正方形数，这是因为这些数目的点子可以排成一个正方形（如图）．试求第n个正方形数是（ ）| A、n（n-1） |
| B、n（n+1） |
| C、n2 |
| D、（n+1）2 |
过椭圆
+
=1（a＞b＞0）左焦点F1作垂直于x轴的直线交椭圆于AB两点，若△ABF2为等边三角形，则该椭圆离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．则P（ξ=0）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（1+x）2n+1的展开式中，二项式系数最大的项所在的项数是（ ）
| A、n，n+1 |
| B、n-1，n |
| C、n+1，n+2 |
| D、n+2，n+3 |