题目内容

某校有学生2000人，其中高一年纪的学生与高三年级的学生之比为3：4，从中抽取一个容量为40的样本，高二年级恰好抽取了12人．求各年级的人数及高一年级、高三年级各抽取的人数．
考点：分层抽样方法
专题：概率与统计
分析：由题意可是分别抽取了3x和4x人，可得方程3x+4x+12=40，解方程可得．
解答： 解：由题意设高一年级的学生与高三年级的学生分别抽取了3x和4x人，
则3x+4x+12=40，解得x=4，
∴高一年级的学生与高三年级的学生分别抽取了12和16人，
点评：本题考查分层抽样，按比例抽取是分层抽样的特点，属基础题．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ）在同一周期内，当x=
π
12
时，取得最大值y=3，当x=
7π
12
时，取得最小值y=-3，则函数的解析式为（　　）
A、y=3sin（2x-
π
3
）
B、y=3sin（
x
2
-
π
6
）
C、y=3sin（2x+
π
6
）
D、y=3sin（2x+
π
3
）
过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）左焦点F1作垂直于x轴的直线交椭圆于AB两点，若△ABF2为等边三角形，则该椭圆离心率为（　　）
A、
1
2
B、
3
3
C、
2
2
D、
1
3
（1+x）2n+1的展开式中，二项式系数最大的项所在的项数是（　　）
A、n，n+1
B、n-1，n
C、n+1，n+2
D、n+2，n+3
函数f（x）=2x3+3x-3的零点所在的区间为（　　）
A、（-1，0）
B、（0，1）
C、（1，2）
D、（2，3）
已知等差数列{an}的前n项和为Sn=n2+pn+q（p，q∈R），且a2，a3，a5成等比数列．
（1）求p，q的值；
（2）若数列{bn}满足an+log2n=log2bn，求数列{bn}的前n项和Tn．
已知等比数列{an}满足a1a2=2a3，且a1，a2+2，a3成等差数列．数列{bn}满足b1log2a1+b2log2a2+…+bnlog2an=
n(n+1)
2
（n∈N*）
（1）求数列{an}和{bn}的通项公式．
（2）求证：
n
2(n+2)
＜
n
k=1
（1-
bk
bk+1
）
1
bk+1
＜
5
6
（n∈N*）．
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，两种坐标系取相同单位长度．已知曲线C：ρ=a（a＞0），过点P（0，2）的直线l的参数方程为
x=
t
2
y=2+
3
2
t
（t为参数）．
（Ⅰ）求曲线C与直线l的普通方程；
（Ⅱ）设曲线C经过伸缩变换
x′=2x
y′=y
得到曲线C′，若直线l与曲线C′相切，求实数a的值．
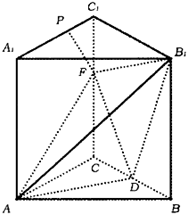在直三棱柱ABC-A1B1C1中，AB=AC═3，BC=2，D是BC的中点，F是上一点，且CF=2．
（1）求证：B1F⊥平面ADF；
（2）若
C1P
=
1
3
C1A1
，求证：PF∥面ADB1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网