题目内容

18．如图，ABCDEF是边长为2的正六边形，则下列命题成立的是（　　）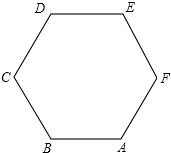
A．$\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$B．$\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$C．$\overrightarrow{BD}$•$\overrightarrow{FD}$=0D．$\overrightarrow{CD}$•（$\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$）=-6

分析 利用正六边形的性质和向量的有关知识逐个分析选项判断．

解答 解：四边形CAFE不是平行四边形，∴$\overrightarrow{CA}+\overrightarrow{CE}$≠$\overrightarrow{CF}$，故A错误；
 $\overrightarrow{CE}-\overrightarrow{AF}$=$\overrightarrow{CE}-\overrightarrow{CD}$=$\overrightarrow{DE}$=-$\overrightarrow{AB}$，故B错；
∵△BDF是等边三角形，∴BD与FD不垂直，∴$\overrightarrow{BD}•\overrightarrow{FD}$≠0，故C错误；
连结FB，则BF=2$\sqrt{3}$，∠AFB=30°，∴$\overrightarrow{CD}•$（$\overrightarrow{AB}-\overrightarrow{AE}-\overrightarrow{EF}$）=$\overrightarrow{CD}•$$\overrightarrow{FB}$=$\overrightarrow{AF}•\overrightarrow{FB}$=2$\sqrt{3}$×2×cos150°=-6．故D正确．
故选D．

点评 本题考查了平面向量的数量积运算，向量的线性运算的几何意义，正六边形的性质，属于基础题．

练习册系列答案
相关题目
8．已知0＜x＜$\frac{π}{2}$，则函数$f（x）={3^{{{sin}^2}x}}+{3^{{{cos}^2}x}}$的最小值是2$\sqrt{3}$．
9．[2sin50°+sin10°（1+$\sqrt{3}$tan10°）]•$\sqrt{2si{n}^{2}80°}$的值为$\sqrt{6}$．
6．设△ABC的内角A，B，C所对的边分别为a，b，c，若acosB+bcosA=csinC，则△ABC的形状为（　　）
A．锐角三角形B．等腰直角三角形C．钝角三角形D．直角三角形
13．已知命题p：点M（1，3）不在圆（x+m）2+（y-m）2=16的内部，
命题q：“曲线${C_1}：\frac{x^2}{m^2}+\frac{y^2}{2m+8}=1$表示焦点在x轴上的椭圆”，
命题s：“曲线${C_2}：\frac{x^2}{m-t}+\frac{y^2}{m-t-1}=1$表示双曲线”．
（1）若“p且q”是真命题，求m的取值范围；
（2）若?s是?q的必要不充分条件，求t的取值范围．
3．函数f（x）=excosx在点（0，f（0））处的切线方程是（　　）
A．x+y+1=0B．x+y-1=0C．x-y+1=0D．x-y-1=0
10．已知定义域为R的奇函数y=f（x）的导函数为y=f′（x），当x≠0时，$f′（x）+\frac{f（x）}{x}$＞0，若a=f（1），b=-2f（-2），c=（ln$\frac{1}{2}$）f（ln$\frac{1}{2}$），则a，b，c的大小关系正确的是（　　）
A．a＜c＜bB．b＜c＜aC．a＜b＜cD．c＜a＜b
7．若存在一数列的前n项为nan，则称该数列为数列{an}的“一阶衍生数列”，记作{（an）1}；同样的，若存在一数列的前n项和为n（an）1，则称该数列为数列{an}的“二阶衍生数列”，记作{（an）2}．记（am）k为数列{an}的“k阶衍生数列”中的第m项．己知等差数列{an}的通项公式为an=2n-1．
（1）写出数列{（a2）n-1}的前四项；
（2）求证：对任意给定的m≥2且m∈N+，数列{（am）n-1}为等比数列．
8．设f（x）是定义在R上的增函数，且对任意x，都有f（-x）+f（x）=0恒成立，如果实数m，n满足不等式f（m2-6m+21）+f（n2-8n）＜0，那么m2+n2的取值范围是（　　）
A．（9，49）B．（13，49）C．（9，25）D．（3，7）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网