题目内容
10.已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,$f′(x)+\frac{f(x)}{x}$>0,若a=f(1),b=-2f(-2),c=(ln$\frac{1}{2}$)f(ln$\frac{1}{2}$),则a,b,c的大小关系正确的是( )| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | c<a<b |
分析 根据a,b,c的表示形式构造函数g(x)=xf(x),根据条件可说明x>0时,g′(x)>0,这便得到g(x)在(0,+∞)上单调递增.而由f(x)为奇函数便可得到b=2f(2),c=(ln2)f(ln2),而容易判断ln2<1<2,从而得到g(ln2)<g(1)<g(2),这样便可得出a,b,c的大小关系.
解答 解:设g(x)=xf(x),$g′(x)=f(x)+xf′(x)=x[f′(x)+\frac{f(x)}{x}]$;
∵x≠0时,$f′(x)+\frac{f(x)}{x}>0$;
∴x>0时,g′(x)>0;
∴g(x)在(0,+∞)上单调递增;
∵f(x)为奇函数;
∴b=-2f(-2)=2f(2),$c=(ln\frac{1}{2})f(ln\frac{1}{2})=(-ln2)f(-ln2)=(ln2)f(ln2)$;
又a=f(1)=1f(1);
∵ln2<1<2,g(x)在(0,+∞)上单调递增;
∴g(ln2)<g(1)<g(2);
即(ln2)f(ln2)<1f(1)<2f(2);
∴c<a<b.
故选:D.
点评 考查构造函数解决问题的方法,会求积的导数,根据导数符号判断函数单调性的方法,以及奇函数的定义,增函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.函数f(x)=log3x+x-5的一个零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
18.如图,ABCDEF是边长为2的正六边形,则下列命题成立的是( )
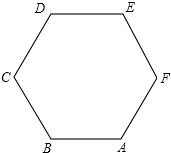

| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |
2.已知偶函数f(x)在[0,+∞)上是增函数,且f(2)=0,则不等式f(x+1)<0的解集是( )
| A. | [0,2) | B. | (-2,2) | C. | (-1,3) | D. | (-3,1) |
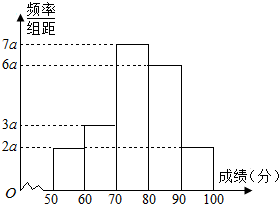 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
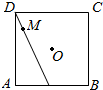
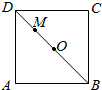
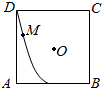
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)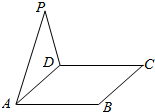 如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )