题目内容
9.[2sin50°+sin10°(1+$\sqrt{3}$tan10°)]•$\sqrt{2si{n}^{2}80°}$的值为$\sqrt{6}$.分析 由条件利用三角恒等变换化简所给的式子可得结果.
解答 解:[2sin50°+sin10°(1+$\sqrt{3}$tan10°)]•$\sqrt{2si{n}^{2}80°}$
=[2sin50°+sin10°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$]•$\sqrt{2}$cos10°
=[2sin50°+2sin10°•$\frac{\frac{1}{2}cos10°+\frac{\sqrt{3}}{2}sin10°}{cos10°}$]•$\sqrt{2}$cos10°
=2$\sqrt{2}$[sin50°cos10°+sin10°•cos(60°-10°)]=2$\sqrt{2}$sin(50°+10°)
=2$\sqrt{2}$sin60°=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题主要考查三角恒等变换,属于中档题.

练习册系列答案
相关题目
13.已知数列{an}满足an>1,过点(an,0)的直线ln与圆x2+y2=1在第一象限相切于点Pn,若记Pn的横坐标为bn,则$\frac{{a}_{1}{b}_{1}+{a}_{2}{b}_{2}+..+{a}_{n}{b}_{n}}{({a}_{1}{a}_{2}…{a}_{n})({b}_{1}{b}_{2}…{b}_{n})}$等于( )
| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
1.函数f(x)=log3x+x-5的一个零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
18.如图,ABCDEF是边长为2的正六边形,则下列命题成立的是( )
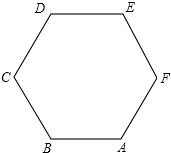

| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |
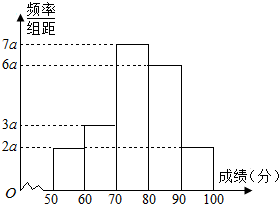 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)