题目内容
8.已知0<x<$\frac{π}{2}$,则函数$f(x)={3^{{{sin}^2}x}}+{3^{{{cos}^2}x}}$的最小值是2$\sqrt{3}$.分析 利用基本不等式的性质即可得出.
解答 解:∵0<x<$\frac{π}{2}$,
则函数$f(x)={3^{{{sin}^2}x}}+{3^{{{cos}^2}x}}$≥2$\sqrt{{3}^{si{n}^{2}x+co{s}^{2}x}}$=2$\sqrt{3}$,当且仅当sin2x=cos2x,x=$\frac{π}{4}$时取等号.
∴函数$f(x)={3^{{{sin}^2}x}}+{3^{{{cos}^2}x}}$的最小值是2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了基本不等式的性质、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.已知数列{an}满足an>1,过点(an,0)的直线ln与圆x2+y2=1在第一象限相切于点Pn,若记Pn的横坐标为bn,则$\frac{{a}_{1}{b}_{1}+{a}_{2}{b}_{2}+..+{a}_{n}{b}_{n}}{({a}_{1}{a}_{2}…{a}_{n})({b}_{1}{b}_{2}…{b}_{n})}$等于( )
| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
3.若a=30.5,b=logπ3,c=log30.5,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
13.若存在x∈(0,+∞),使不等式ex(x2-x+1)(ax+3a-1)<1成立,则( )
| A. | 0$<a<\frac{1}{3}$ | B. | a$<\frac{2}{e+1}$ | C. | a$<\frac{2}{3}$ | D. | a$<\frac{1}{3}$ |
18.如图,ABCDEF是边长为2的正六边形,则下列命题成立的是( )
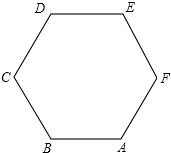

| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |