函数f(x)=excosx在点处的切线方程是( )A．x+y+1=0B．x+y-1=0C．x-y+1=0D．x-y-1=0 题目和参考答案——青夏教育精英家教网—

题目内容

3．函数f（x）=e^xcosx在点（0，f（0））处的切线方程是（　　）

A．

x+y+1=0

B．

x+y-1=0

C．

x-y+1=0

D．

x-y-1=0

分析求出函数的导数，求得切线的斜率和切点坐标，由点斜式方程可得所求切线的方程．

解答解：函数f（x）=e^xcosx的导数为f′（x）=e^x（cosx-sinx），
即有在点（0，f（0））处的切线斜率为k=e⁰（cos0-sin0）=1，
切点为（0，1），
则在点（0，f（0））处的切线方程为y-1=x-0，即为x-y+1=0．
故选C．

点评本题考查导数的运用：求切线的方程，注意运用导数的几何意义和直线的方程，考查运算能力，属于基础题．

练习册系列答案

14．已知数列{a_n}满足：S_n=1-a_n（n∈N^*），其中S_n为数列{a_n}的前n项和．则{a_n}的通项公式为${a}_{n}=\frac{1}{{2}^{n}}$．

11．函数y=f（x）与函数y=g（x）互为反函数，且f（x）=2^x，则函数y=g（x²-1）的定义域是（-∞，-1）∪（1，+∞）．

18．如图，ABCDEF是边长为2的正六边形，则下列命题成立的是（　　）

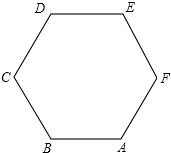
A．

$\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$

B．

$\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$

C．

$\overrightarrow{BD}$•$\overrightarrow{FD}$=0

D．

$\overrightarrow{CD}$•（$\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$）=-6

8．已知变量x，y满足$\left\{{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}}\right.$，则$\frac{x+y+3}{x+2}$的取值范围是（　　）

A．

$[{2，\frac{5}{2}}]$

B．

$[{\frac{5}{4}，\frac{5}{2}}]$

C．

$[{\frac{4}{5}，\frac{5}{2}}]$

D．

$[{\frac{5}{4}，2}]$

15．集合A={0，2，a}，B={1，a}，若A∪B={0，1，2，4}，则a的值为4．

12．已知函数f（x）=aln（x-a）-$\frac{1}{2}$x²+x（a＜0）．
（1）当a=-2时，求f（x）在[-$\frac{3}{2}$，2]上的最小值（参考数据：ln2=0.6931）；
（2）若函数f（x）有且仅有一个零点，求实数a的取值范围．

13．已知三个不同的平面α、β、γ和两条不同的直线m、n，有下列五个命题：
①若m∥n，m⊥α，则n⊥α；　　　　　　　　　　　　　②若m⊥α，m⊥β，则α∥β
③若m⊥α，m∥n，n?β，则α⊥β；　　　　　　　　　　　④若m∥α，α∩β=n，则则m∥n
⑤若α⊥γ，β⊥γ，且α∩β=m，则m⊥γ．
其中正确命题的编号是①②③④⑤．

试题分类