题目内容
8.设f(x)是定义在R上的增函数,且对任意x,都有f(-x)+f(x)=0恒成立,如果实数m,n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是( )| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
分析 根据对于任意的x都有f(-x)+f(x)=0恒成立,不等式可化为f(m2-6m+21)<f(-n2+8n),利用f(x)是定义在R上的增函数,可得(m-3)2+(n-4)2<4,确定(m-3)2+(n-4)2=4内的点到原点距离的取值范围,利用m2+n2 表示(m-3)2+(n-4)2=4内的点到原点距离的平方,即可求得m2+n2 的取值范围.
解答 解:∵对于任意的x都有f(-x)+f(x)=0恒成立,
∴f(-x)=-f(x),
∵f(m2-6m+21)+f(n2-8n)<0,
∴f(m2-6m+21)<-f(n2-8n)=f(-n2+8n),
∵f(x)是定义在R上的增函数,
∴m2-6m+21<-n2+8n,
∴(m-3)2+(n-4)2<4
∵(m-3)2+(n-4)2=4的圆心坐标为:(3,4),半径为2,
∴(m-3)2+(n-4)2=4内的点到原点距离的取值范围为(5-2,5+2),即(3,7),
∵m2+n2 表示(m-3)2+(n-4)2=4内的点到原点距离的平方,
∴m2+n2 的取值范围是(9,49).
故选:A.
点评 本题考查函数的奇偶性与单调性,考查不等式的含义,解题的关键是确定圆内的点到原点距离的取值范围.

练习册系列答案
相关题目
18.如图,ABCDEF是边长为2的正六边形,则下列命题成立的是( )
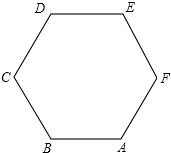

| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为$\sqrt{2}$,则其渐近线方程为( )
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{{\sqrt{2}}}{2}x$ | D. | $y=±\frac{1}{2}x$ |
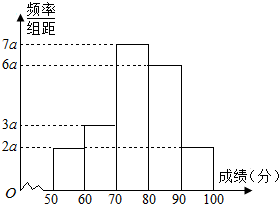 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
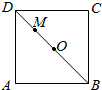
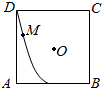
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)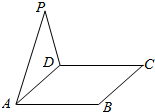 如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
如图,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )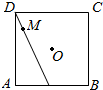

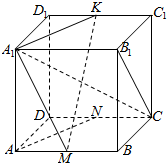 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证: