��Ŀ����
13����֪����p����M��1��3������Բ��x+m��2+��y-m��2=16���ڲ�������q��������${C_1}��\frac{x^2}{m^2}+\frac{y^2}{2m+8}=1$��ʾ������x���ϵ���Բ����
����s��������${C_2}��\frac{x^2}{m-t}+\frac{y^2}{m-t-1}=1$��ʾ˫���ߡ���
��1������p��q���������⣬��m��ȡֵ��Χ��
��2����?s��?q�ı�Ҫ�������������t��ȡֵ��Χ��
���� ��1����pΪ�棺��1+m��2+��3-m��2��16��������m��Χ����qΪ�棺��$\left\{{\begin{array}{l}{{m^2}��2m+8}\\{2m+8��0}\end{array}}\right.$�����m��Χ������p��q���������⣬��������Χ�������ɵó���
��2����sΪ�棬��m-t����m-t-1����0����?s��?q�ı�Ҫ�������������q��s�ı�Ҫ�����������������ɵó���
��� �⣺��1����pΪ�棺��1+m��2+��3-m��2��16�����m��-1��m��3��
��qΪ�棺��$\left\{{\begin{array}{l}{{m^2}��2m+8}\\{2m+8��0}\end{array}}\right.$�����-4��m��-2��m��4��
����p��q���������⣬��$\left\{{\begin{array}{l}{m��-1��m��3}\\{-4��m��-2��m��4}\end{array}}\right.$�����-4��m��-2��m��4��
��2����sΪ�棬��m-t����m-t-1����0����t��m��t+1��
��?s��?q�ı�Ҫ�������������q��s�ı�Ҫ�����������
��ɵ�{m|t��m��t+1}?{m|-4��m��-2��m��4}����$\left\{{\begin{array}{l}{t��-4}\\{t+1��-2}\end{array}}\right.$��t��4
���-4��t��-3��t��4��
���� ���⿼����Բ���ߵı����̼������ʡ�����ʽ�Ľⷨ�������ʡ����������ж�������������������������������������е��⣮

| A�� | a��b��c | B�� | b��a��c | C�� | c��a��b | D�� | b��c��a |
| A�� | ��0��1�� | B�� | ��1��2�� | C�� | ��2��3�� | D�� | ��3��4�� |
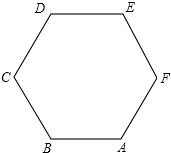
| A�� | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B�� | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C�� | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D�� | $\overrightarrow{CD}$•��$\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$��=-6 |
| A�� | [0��2�� | B�� | ��-2��2�� | C�� | ��-1��3�� | D�� | ��-3��1�� |
| A�� | y=��x | B�� | $y=��\sqrt{2}x$ | C�� | $y=��\frac{{\sqrt{2}}}{2}x$ | D�� | $y=��\frac{1}{2}x$ |