题目内容
已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3);
(1)若数列{bn}满足bn=an-3an-1(n≥2),求数列{bn}的通项公式bn;
(2)求数列{an}的通项公式.
(1)若数列{bn}满足bn=an-3an-1(n≥2),求数列{bn}的通项公式bn;
(2)求数列{an}的通项公式.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)根据递推数列,构造数列,利用等比数列的定义和通项公式即可,即可求数列{bn}的通项公式bn;
(2)利用递推数列,构成一个新的等比数列,两式联立即可得到结论.
(2)利用递推数列,构成一个新的等比数列,两式联立即可得到结论.
解答:
解:(1)∵a1=5,a2=2,an=2an-1+3an-2(n≥3);
∴an-3an-1=-(an-1-3an-2),
即{an-3an-1}是公比q=-1的等比数列,首项a2-3a1=2-15=-13,
即{bn}的通项公式bn=-13×(-1)n-1.
(2)∵a1=5,a2=2,an=2an-1+3an-2(n≥3);
∴an+an-1=3an-1+3an-2=3(an-1+an-2),
即{an+an-1}是公比前=3的等比数列,首项a2+a1=5+2=7,
∴an+an-1=7×3n-1,①
由(1)得an-3an-1=-13×(-1)n-1.②,
①×3+①得,
4an=3×7×3n-1-13×(-1)n-1.
即an=
[7×3n+13×(-1)n].
∴an-3an-1=-(an-1-3an-2),
即{an-3an-1}是公比q=-1的等比数列,首项a2-3a1=2-15=-13,
即{bn}的通项公式bn=-13×(-1)n-1.
(2)∵a1=5,a2=2,an=2an-1+3an-2(n≥3);
∴an+an-1=3an-1+3an-2=3(an-1+an-2),
即{an+an-1}是公比前=3的等比数列,首项a2+a1=5+2=7,
∴an+an-1=7×3n-1,①
由(1)得an-3an-1=-13×(-1)n-1.②,
①×3+①得,
4an=3×7×3n-1-13×(-1)n-1.
即an=
| 1 |
| 4 |
点评:本题主要考查数列的通项公式的求法,利用递推数列进行构造两个等比数列是解决本题的关键,综合性较强,运算量较大.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=3x+2y的最大值为( )
|
| A、10 | B、8 | C、7 | D、2 |
“x≥1”是“x+
≥2”( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |
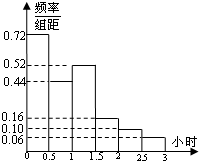 电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.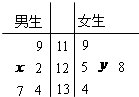 某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.
某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.