题目内容
在10支铅笔中，有8支正品和2支次品，现从中任取1支，则取得次品的概率是多少？
考点：古典概型及其概率计算公式
专题：概率与统计
分析：从中任取1支共有10种取法，取得次品共2种取法，由概率公式可得．
解答：
解：在10支铅笔中，有8支正品和2支次品，
现从中任取1支共有10种取法，取得次品共2种取法，
∴取得次品的概率P=
=
现从中任取1支共有10种取法，取得次品共2种取法，
∴取得次品的概率P=
| 2 |
| 10 |
| 1 |
| 5 |
点评：本题考查古典概型及其概率公式，属基础题．
练习册系列答案
相关题目
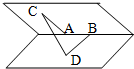如图在一个二面角的棱上有两个点A，B，线段AC，BD分别在这个二面角的两个面内，并且都垂直于棱AB，AB=4cm，AC=6cm，BD=8cm，CD=2| 17 |
| A、30° | B、60° |
| C、90° | D、120° |
已知m，n是两条不同直线，α，β是两个不同的平面，且n?β，则下列叙述正确的是（ ）
| A、若m∥n，m?α，则α∥β |
| B、若α∥β，m?α，则m∥n |
| C、若m∥n，m⊥α，则α⊥β |
| D、若α∥β，m⊥n，则m⊥α |
已知直线x-2y-a=0与圆：x2+y2+2x-4y=0相切，则a=（ ）
| A、0 | B、-10或0 |
| C、-3或0 | D、--10 |