题目内容
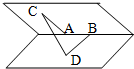如图在一个二面角的棱上有两个点A，B，线段AC，BD分别在这个二面角的两个面内，并且都垂直于棱AB，AB=4cm，AC=6cm，BD=8cm，CD=2| 17 |
| A、30° | B、60° |
| C、90° | D、120° |
考点：二面角的平面角及求法
专题：空间位置关系与距离,空间角
分析：首先利用平行线做出二面角的平面角，进一步利用勾股定理和余弦定理解出二面角平面角的大小，最后确定结果．
解答：
解：在平面α内做BE∥AC，BE=AC，连接DE，CE，
所以四边形ACEB是平行四边形．
由于线段AC，BD分别在这个二面角的两个面内，并且都垂直于棱AB，
所以AB⊥平面BDE．
CE∥AB
CE⊥平面BDE．
所以△CDE是直角三角形．
又AB=4cm，AC=6cm，BD=8cm，CD=2
cm，
则：DE=2
cm
进一步利用余弦定理：DE2=BE2+BD2-2BE•BDcos∠DBE
解得cos∠DBE=
所以∠DBE=60°
即二面角的度数为：60°
故选：B
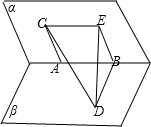
所以四边形ACEB是平行四边形．
由于线段AC，BD分别在这个二面角的两个面内，并且都垂直于棱AB，
所以AB⊥平面BDE．
CE∥AB
CE⊥平面BDE．
所以△CDE是直角三角形．
又AB=4cm，AC=6cm，BD=8cm，CD=2
| 17 |
则：DE=2
| 13 |
进一步利用余弦定理：DE2=BE2+BD2-2BE•BDcos∠DBE
解得cos∠DBE=
| 1 |
| 2 |
所以∠DBE=60°
即二面角的度数为：60°
故选：B
点评：本题考查的知识要点：余弦定理的应用，勾股定理的应用，线面垂直的性质，二面角的应用．属于基础题型．
练习册系列答案
天天练口算系列答案
相关题目
下列判断错误的是（ ）
| A、“am2＜bm2”是“a＜b”的充分不必要条件 |
| B、若f′（x0）=0，则x=x0是函数y=f（x）的极值点 |
| C、函数y=f（x）满足f（x+1）=f（1-x），则其图象关于直线x=1对称 |
| D、定义在R上的函数y=f（x）满足f（x+1）=-f（x），则周期为2 |
已知某几何体的三视图如图，则该几何体是 （ ）
| A、圆柱 | B、圆锥 | C、圆台 | D、球 |
函数g（x）=log2x，关于方程|g（x）|2+m|g（x）|+2m+3=0在（0，2）内有三个不同的实数解，则实数m的取值范围是（ ）
A、（-∞，4-2
| ||||
B、（4-2
| ||||
C、（-
| ||||
D、（-
|