题目内容
已知集合M={1,2,3,…,100},A是集合M的非空子集,把集合A中的各元素之和记作S(A).
①满足S(A)=8的集合A的个数为 ;
②S(A)的所有不同取值的个数为 .
①满足S(A)=8的集合A的个数为
②S(A)的所有不同取值的个数为
考点:元素与集合关系的判断
专题:集合
分析:①用列举法逐一列出可能的情形即可;
②根据S(A)的所有可能取值情况,从而得到其所有不同取值的个数.
②根据S(A)的所有可能取值情况,从而得到其所有不同取值的个数.
解答:
解:①一个元素:8;两个元素:1,7;2,6;3,5;三个元素:1,3,4;1,2,5;四个元素:
∴满足S(A)=8的集合A的个数为6.
②∵S(A)的所有可能取值为1,2,3,4,5,…,100.
对于S(A)来说,由于它是集合A中的各元素之和,同时
A又是集合M的非空子集,
∵1+2+3+…+100=5050,
∴易知S(A)将取尽1到5050的所有数,
∴S(A)的取值个数为5050,
故答案:①6;②5050.
∴满足S(A)=8的集合A的个数为6.
②∵S(A)的所有可能取值为1,2,3,4,5,…,100.
对于S(A)来说,由于它是集合A中的各元素之和,同时
A又是集合M的非空子集,
∵1+2+3+…+100=5050,
∴易知S(A)将取尽1到5050的所有数,
∴S(A)的取值个数为5050,
故答案:①6;②5050.
点评:本题重点考查集合的基本概念,集合的元素特征等知识,考查角度比较新颖,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
函数y=2+
sinx的最小正周期和最小值分别为( )
| 2 |
| A、π,1 | ||
| B、2π,1 | ||
C、π,2-
| ||
D、2π,2-
|
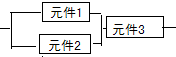 某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为
某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为