题目内容
已知等差数列{an}的公差d≠0,它的前n项和为Sn,若s5=70,且a2,a7,a22成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{
}的前n项和为Tn,求证:Tn<2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{
| an+6 |
| (n+1)Sn |
考点:数列的求和,等差数列的通项公式,等差数列的性质
专题:等差数列与等比数列
分析:解:(Ⅰ)以题意,由前n项和公式及通项公式列出方程组
求出a1=6,d=4,用公式求出数列{an}的通项公式.
(Ⅱ)证明:由(Ⅰ)求出
=
=
利用裂项相消求出前n项和为Tn,证出不等式.
|
(Ⅱ)证明:由(Ⅰ)求出
| an+6 |
| (n+1)Sn |
| 4n+2+6 |
| (n+1)(2n2+4n) |
| 4(n+2) |
| 2n(n+1)(n+2) |
| 2 |
| n(n+1) |
解答:
解:(Ⅰ)依题意,有
即
解得a1=6,d=4,
∴数列{an}的通项公式an=4n+2;
(Ⅱ)证明:由(Ⅰ)可得Sn=2n2+4n,
∴
=
=
,
∴Tn=2[(1-
)+(
-
)+…+(
-
)]
=2(1-
),∵
>0
∴Tn=2(1-
)<2.
|
即
|
解得a1=6,d=4,
∴数列{an}的通项公式an=4n+2;
(Ⅱ)证明:由(Ⅰ)可得Sn=2n2+4n,
∴
| an+6 |
| (n+1)Sn |
| 4n+2+6 |
| (n+1)(2n2+4n) |
| 4(n+2) |
| 2n(n+1)(n+2) |
| 2 |
| n(n+1) |
∴Tn=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
| 1 |
| n+1 |
∴Tn=2(1-
| 1 |
| n+1 |
点评:本题考查等差数列的通项公式及前n项和公式;考查数列求和的方法常考的求和的方法有错位相减法和裂项相消法.

练习册系列答案
相关题目
在区间[-3,3]上任取两数x,y,使x2-y-1<0成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2|sinx|是( )
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为π的偶函数 |
 如图所示,扇形AOB,圆心角AOB的大小等于
如图所示,扇形AOB,圆心角AOB的大小等于
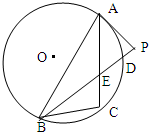 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.