题目内容
已知函数:f(x)=
(a∈R且x≠a).
(1)证明:f(x)+2+f(2a-x)=0对定义域内所有x都成立;
(2)若函数g(x)=x2+|(x-a)f(x)|在[a,a+1]的最小值为4,求a的值.
| x+1-a |
| a-x |
(1)证明:f(x)+2+f(2a-x)=0对定义域内所有x都成立;
(2)若函数g(x)=x2+|(x-a)f(x)|在[a,a+1]的最小值为4,求a的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)将f(x)和f(2a-x)代入整理即可,
(2)将x分区间进行讨论,通过找到单调区间求最值.
(2)将x分区间进行讨论,通过找到单调区间求最值.
解答:
解(1)证明:f(x)+2+f(2a-x)=
+2+
=
+2+
=
=0
∴命题得证.
(2)g(x)=x2+|x+1-a|(x≠a)
1)当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+
)2+
-a
如果a-1≥-
即a≥
时,
则函数在[a-1,a)和(a,+∞)上单调递增
g(x)min=g(a-1)=(a-1)2
如果a-1<-
即当a<
且a≠-
时,g(x)min=g(-
)=
-a
当a=-
时,g(x)最小值不存在;
2)当x≤a-1时g(x)=x2-x-1+a=(x-
)2+a-
如果a-1>
即a>
时g(x)min=g(
)=a-
如果a-1≤
即a≤
时g(x)在(-∞,a-1)上为减函数g(x)min=g(a-1)=(a-1)2,
当a>
时(a-1)2-(a-
)=(a-
)2>0,当a<
时(a-1)2-(
-a)=(a-
)2>0
综合得:当a<
且a≠-
时 g(x)最小值是
-a
当
≤a≤
时 g(x)最小值是(a-1)2;
当a>
时 g(x)最小值为a-
当a=-
时 g(x)最小值不存在.
| x+1-a |
| a-x |
| 2a-x+1-a |
| a-2a+x |
=
| x+1-a |
| a-x |
| a-x+1 |
| x-a |
| x+1-a+2a-2x-a+x-1 |
| a-x |
∴命题得证.
(2)g(x)=x2+|x+1-a|(x≠a)
1)当x≥a-1且x≠a时,g(x)=x2+x+1-a=(x+
| 1 |
| 2 |
| 3 |
| 4 |
如果a-1≥-
| 1 |
| 2 |
| 1 |
| 2 |
则函数在[a-1,a)和(a,+∞)上单调递增
g(x)min=g(a-1)=(a-1)2
如果a-1<-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当a=-
| 1 |
| 2 |
2)当x≤a-1时g(x)=x2-x-1+a=(x-
| 1 |
| 2 |
| 5 |
| 4 |
如果a-1>
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
如果a-1≤
| 1 |
| 2 |
| 3 |
| 2 |
当a>
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
综合得:当a<
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当
| 1 |
| 2 |
| 3 |
| 2 |
当a>
| 3 |
| 2 |
| 5 |
| 4 |
当a=-
| 1 |
| 2 |
点评:本题考查了二次函数的性质,恒等式的证明,求单调区间,求最值问题,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
二项式(x2+
)10展开式中的常数项是( )
| 2 | ||
|
| A、第7项 | B、第8项 |
| C、第9项 | D、第10项 |
已知随机变量Z服从正态分布N(0,σ2),若P(Z>1)=0.023,则P(-1≤Z≤1)=( )
| A、0.625 |
| B、0.954 |
| C、0.477 |
| D、0.977 |
 如图所示,扇形AOB,圆心角AOB的大小等于
如图所示,扇形AOB,圆心角AOB的大小等于
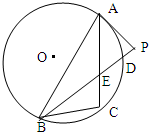 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.