题目内容
已知函数f(x)=2sin2(
+x)-
cos2x.
(1)求f(x)的单调减区间;
(2)求f(x)在x∈[
,
]上的值域;
(3)若不等式|f(x)-m|<2在x∈[
,
]上恒成立,求实数m的取值范围.
| π |
| 4 |
| 3 |
(1)求f(x)的单调减区间;
(2)求f(x)在x∈[
| π |
| 4 |
| π |
| 2 |
(3)若不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的定义域和值域,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)首先,根据二倍角公式化简函数解析式:f(x)=2sin(2x-
)+1,然后,结合三角函数的单调性进行求解;
(2)直接根据x∈[
,
],得到∴(2x-
)∈[
,
],从而得到f(x)在x∈[
,
]上的值域;
(3)根据|f(x)-m|<2,得到m-2<f(x)<m+2,然后根据恒成立问题,得到
,从而得到实数m的取值范围.
| π |
| 3 |
(2)直接根据x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 4 |
| π |
| 2 |
(3)根据|f(x)-m|<2,得到m-2<f(x)<m+2,然后根据恒成立问题,得到
|
解答:
解:(1)∵函数f(x)=2sin2(
+x)-
cos2x
=1-cos(
+2x)-
cos2x
=sin2x-
cos2x+1
=2sin(2x-
)+1,
∴f(x)=2sin(2x-
)+1,
令
+2kπ≤2x-
≤
+2kπ,k∈Z,
∴x∈[
+kπ,
+kπ],(k∈Z)
∴f(x)的单调减区间是[
+kπ,
+kπ] (k∈Z)
(2)∵x∈[
,
],
∴2x∈[
,π],
∴(2x-
)∈[
,
],
∴2sin(2x-
)∈[1,2],
∴f(x)∈[2,3],
∴f(x)值域是[2,3]
(3)∵|f(x)-m|<2,
∴m-2<f(x)<m+2,
∵不等式|f(x)-m|<2在x∈[
,
]上恒成立,
∴
,
∴1<m<4,
∴实数m的取值范围是1<m<4.
| π |
| 4 |
| 3 |
=1-cos(
| π |
| 2 |
| 3 |
=sin2x-
| 3 |
=2sin(2x-
| π |
| 3 |
∴f(x)=2sin(2x-
| π |
| 3 |
令
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
∴x∈[
| 5π |
| 12 |
| 11π |
| 12 |
∴f(x)的单调减区间是[
| 5π |
| 12 |
| 11π |
| 12 |
(2)∵x∈[
| π |
| 4 |
| π |
| 2 |
∴2x∈[
| π |
| 2 |
∴(2x-
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴2sin(2x-
| π |
| 3 |
∴f(x)∈[2,3],
∴f(x)值域是[2,3]
(3)∵|f(x)-m|<2,
∴m-2<f(x)<m+2,
∵不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
∴
|
∴1<m<4,
∴实数m的取值范围是1<m<4.
点评:本题综合考查了三角公式、三角恒等变换公式、恒成立问题、二倍角公式等知识,属于中档题.

练习册系列答案
相关题目
复数z=
,
是z的共轭复数,则z+
=( )
| 2i |
| 1+i |
. |
| z |
. |
| z |
| A、4 | B、-4 | C、2 | D、-2 |
 如图所示,扇形AOB,圆心角AOB的大小等于
如图所示,扇形AOB,圆心角AOB的大小等于
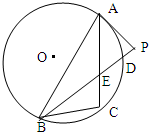 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.