题目内容
已知函数f（x）=x3-12x+8在区间[-5，3]上的最大值与最小值为M，m，求M-m值．
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：根据用导数求闭区间上函数最值的方法：求导数，根据导数符号，判断出函数的极大值点，极小值点比求出极大值与极小值，与端点值比较即可得到函数在这一闭区间上的最值，即可求出函数f（x）的最大值M和最小值m．
解答：
解：f′（x）=3（x2-4）；
∴x∈[-5，-2）时，f′（x）＞0；x∈（-2，2）时，f′（x）＜0；x∈（2，3]时，f′（x）＞0；
∴f（-2）=24是函数f（x）的极大值，f（2）=-8是f（x）的极小值，且f（-5）=-57，f（3）=-1；
∴函数f（x）的最大值M=24，最小值m=-57，
∴M-m=81．
∴x∈[-5，-2）时，f′（x）＞0；x∈（-2，2）时，f′（x）＜0；x∈（2，3]时，f′（x）＞0；
∴f（-2）=24是函数f（x）的极大值，f（2）=-8是f（x）的极小值，且f（-5）=-57，f（3）=-1；
∴函数f（x）的最大值M=24，最小值m=-57，
∴M-m=81．
点评：考查利用导数求函数在一闭区间上的最值的方法：先求导数，判断函数在这一闭区间上的极值点，并求出函数的极值，比较端点值，最大的即为最大值，最小的即为最小值．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
已知一个正方体的8个顶点都在同一个球面上，则球的表面积与这个正方体的全面积之比为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中的假命题是（ ）
| A、?x∈R，x3＞0 |
| B、?x∈R，tanx=1 |
| C、?x∈R，lgx=0 |
| D、?x∈R，2x＞0 |
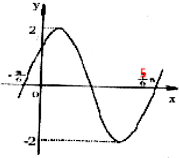如图，已知函数y=Asin（ωx+φ）（A＞0，0＜φ＜π）的图象经过点（-