题目内容
函数f(x)=loga|x+1|,当x∈(-1,0)时,恒有f(x)>0,有( )
| A、f(x)在(-∞,-1)上是增函数 |
| B、f(x)在(-∞,0)上是减函数 |
| C、f(x)在(0,+∞)上是增函数 |
| D、f(x)在(-∞,+∞)上是减函数 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据x的取值范围,结合对数函数的单调性,即可求出0<a<1,然后根据复合函数单调性之间的关系,即可得到结论.
解答:
解:设t=|x+1|,
则当x∈(-1,0)时,t=|x+1|=x+1,为增函数,
且t∈(0,1),
则y=logat,
∵当x∈(-1,0)时,恒有f(x)>0,
即在t∈(0,1),logat>0,
∴0<a<1,
∴此时y=logat为减函数,
∴要使函数f(x)=loga|x+1|为增函数,
则根据复合函数单调性之间的关系可知t=|x+1|为减函数,
∵t=|x+1|在(-∞,-1)上是减函数,
∴f(x)在(-∞,-1)上是增函数,
故选:A.
则当x∈(-1,0)时,t=|x+1|=x+1,为增函数,
且t∈(0,1),
则y=logat,
∵当x∈(-1,0)时,恒有f(x)>0,
即在t∈(0,1),logat>0,
∴0<a<1,
∴此时y=logat为减函数,
∴要使函数f(x)=loga|x+1|为增函数,
则根据复合函数单调性之间的关系可知t=|x+1|为减函数,
∵t=|x+1|在(-∞,-1)上是减函数,
∴f(x)在(-∞,-1)上是增函数,
故选:A.
点评:本题主要考查复合函数单调性的判断和应用,根据条件结合对数函数的图象和性质求出a的取值范围是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=lnx+1可导,则
等于( )
| lim |
| △x→0 |
| f(1+3△x)-f(1) |
| △x |
| A、1 | ||
| B、0 | ||
| C、3 | ||
D、
|
若{an}为等差数列,Sn为其前n项和,且a5+a6+a7=48,则S11的值是( )
| A、176 | B、96 |
| C、256 | D、196 |
下列各角中,终边相同的是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列命题中的假命题是( )
| A、?x∈R,x3>0 |
| B、?x∈R,tanx=1 |
| C、?x∈R,lgx=0 |
| D、?x∈R,2x>0 |
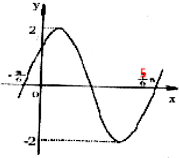 如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-
如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-