题目内容
定义在R上奇函数g(x)与偶函数h(x),对任意x∈R满足g(x)+h(x)=sin2x+sinx+acosx.a为实数
(1)求奇函数g(x)和偶函数f(x)的表达式;
(2)若a>2,求函数h(x)在区间[
,π]上的最值.
(1)求奇函数g(x)和偶函数f(x)的表达式;
(2)若a>2,求函数h(x)在区间[
| π |
| 3 |
考点:三角函数的最值
专题:三角函数的求值
分析:(1)在所给的等式中,用-x代替x,再得到一个等式,由这两个等式解方程组求得g(x)和f(x)的表达式.
(2)根据h(x)=-(cosx-
)2+
+1,对称轴
>1,cosx∈[-1,
],再利用二次函数的性质求得函数h(x)的最值.
(2)根据h(x)=-(cosx-
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵g(x)+h(x)=sin2x+sinx+acosx①,
∴g(-x)+h(-x)=sin2(-x)+sin(-x)+acos(-x)-g(x)+h(x)=sin2x-sinx+acosx②.
联立①②得h(x)=sin2x+acosx,g(x)=sinx.
(2)h(x)=1-cos2x+acosx=-(cosx-
)2+
+1,
若a>2,则对称轴
>1,且x∈[
,π]时,cosx∈[-1,
],
当cosx=-1,h(x)min=-a,当cosx=
,h(x)max=
+
=
.
∴g(-x)+h(-x)=sin2(-x)+sin(-x)+acos(-x)-g(x)+h(x)=sin2x-sinx+acosx②.
联立①②得h(x)=sin2x+acosx,g(x)=sinx.
(2)h(x)=1-cos2x+acosx=-(cosx-
| a |
| 2 |
| a2 |
| 4 |
若a>2,则对称轴
| a |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
当cosx=-1,h(x)min=-a,当cosx=
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 4 |
| 2a+3 |
| 4 |
点评:本题主要考查函数的奇偶性的应用,余弦函数的值域,二次函数的性质,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
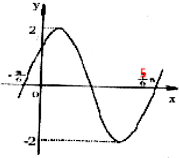 如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-
如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-