题目内容
已知
=(sinωx,
sinωx),
=(sinωx,cosωx)(ω>0),函数f(x)=
•
-
,且f(x)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调递增区间.
| a |
| 3 |
| b |
| a |
| b |
| 1 |
| 2 |
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调递增区间.
考点:两角和与差的正弦函数,平面向量数量积的运算,正弦函数的单调性
专题:三角函数的图像与性质
分析:(Ⅰ)首先,根据辅助角公式,得到f(x)=sin(2ωx-
),然后,结合周期公式求解即可;
(Ⅱ)直接结合正弦函数的单调性进行求解即可.
| π |
| 6 |
(Ⅱ)直接结合正弦函数的单调性进行求解即可.
解答:
解:(Ⅰ)∵f(x)=
•
-
=sin2ωx+
sinωxcosωx-
∴f(x)=
+
sin2ωx-
=
sin2ωx-
cos2ωx
∴f(x)=sin(2ωx-
)…(4分)
∵函数f(x)的最小正周期为π,且ω>0,
∴
=π,解得ω=1…ks5u…(6分)
(Ⅱ)由(Ⅰ)得f(x)=sin(2x-
).
∴欲求f(x)的增区间,
只需 -
+2kπ≤2x-
≤
+2kπ,k∈Z,…(8分)
解得:-
+kπ≤x≤
+kπ,k∈Z…(10分)
∴函数f(x)的单调递增区间为[-
+kπ,
+kπ],k∈Z…(12分)
| a |
| b |
| 1 |
| 2 |
=sin2ωx+
| 3 |
| 1 |
| 2 |
∴f(x)=
| 1-cos2ωx |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
∴f(x)=sin(2ωx-
| π |
| 6 |
∵函数f(x)的最小正周期为π,且ω>0,
∴
| 2π |
| 2ω |
(Ⅱ)由(Ⅰ)得f(x)=sin(2x-
| π |
| 6 |
∴欲求f(x)的增区间,
只需 -
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:-
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调递增区间为[-
| π |
| 6 |
| π |
| 3 |
点评:本题重点考查了三角函数的基本图象与性质、三角恒等变换公式、辅助角公式等知识,属于中档题,也是近几年高考的热点问题.

练习册系列答案
相关题目
i为虚数单位,则z=1+i+i2+…+i10的共轭复数
等于( )
. |
| z |
| A、1-i | B、-i |
| C、-1+i | D、i |
下列各角中,终边相同的是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
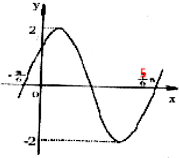 如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-
如图,已知函数y=Asin(ωx+φ)(A>0,0<φ<π)的图象经过点(-