题目内容
12.定圆M:(x+$\sqrt{3}$)2+y2=16,动圆N过点F($\sqrt{3}$,0)且与圆M相切,记圆心N的轨迹为E.求轨迹E的方程.分析 由题意画出图形,利用圆心距与半径的关系可得:|MN|+|MF|=4$>2\sqrt{3}$,从而得M的轨迹E是以M、F为焦点的椭圆,由椭圆的定义可得曲线E的方程.
解答 解:如图,A(-$\sqrt{3}$,0),F($\sqrt{3}$,0),定圆M:(x+$\sqrt{3}$)2+y2=16,动圆N过点F($\sqrt{3}$,0)且与圆M相切,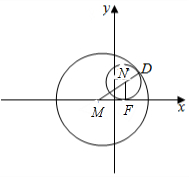
∵|MN|=4-|FM,
可得:|MN|+|MF|=4$>2\sqrt{3}$,
∴N的轨迹E是以M、F为焦点的椭圆,且a=2,c=$\sqrt{3}$,
则b2=a2-c2=1,
∴曲线C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
点评 本题考查轨迹方程的求法,考查了圆与圆位置关系的应用,考查了椭圆的定义,是中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
8.已知数列{an}满足2an+1-an=0,若a2=$\frac{1}{2}$,则数列{an}的前11项和为( )
| A. | 256 | B. | $\frac{1023}{4}$ | C. | $\frac{2047}{1024}$ | D. | $\frac{4095}{2048}$ |
7.设函数y=sin(ωx-$\frac{π}{3}$)cos(ωx-$\frac{π}{3}$)的周期为2,且ω>0,则ω=( )
| A. | 1 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
1.正方体ABCD-A1B1C1D1棱长为6,O点在棱BC上,且BO=2OC,过O点的直线l与直线AA1,C1D1分别交于M,N两点,则MN=( )
| A. | 3$\sqrt{13}$ | B. | 9$\sqrt{5}$ | C. | 14 | D. | 21 |
2.设k1,k2分别是两条直线l1,l2的斜率,则“l1∥l2”是“k1=k2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
