题目内容
4.已知两个单位向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,$\overrightarrow{c}$=(1-t)$\overrightarrow{a}$+t$\overrightarrow{b}$,若$\overrightarrow{b}$•$\overrightarrow{c}$=-$\frac{1}{2}$,则t等于( )| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 可知$|\overrightarrow{a}|=|\overrightarrow{b}|=1,<\overrightarrow{a},\overrightarrow{b}>=60°$,进行数量积的运算即可由$\overrightarrow{b}•[(1-t)\overrightarrow{a}+t\overrightarrow{b}]=-\frac{1}{2}$得出关于t的方程,解出t即可.
解答 解:
$\overrightarrow{b}•\overrightarrow{c}=\overrightarrow{b}•[(1-t)\overrightarrow{a}+t\overrightarrow{b}]$
=$(1-t)\overrightarrow{b}•\overrightarrow{a}+t{\overrightarrow{b}}^{2}$
=$\frac{1-t}{2}+t$
=$-\frac{1}{2}$;
解得t=-2.
故选D.
点评 考查单位向量的概念,向量数量积的运算及计算公式.

练习册系列答案
相关题目
9.若一个正四面体的表面积为S1,其内切球的表面积为S2,则$\frac{S_1}{S_2}$=( )
| A. | $\frac{6}{π}$ | B. | $\frac{{6\sqrt{3}}}{π}$ | C. | $\frac{4}{3}$ | D. | $\frac{{4\sqrt{3}}}{π}$ |
16.在Rt△ABC中,CA=4,CB=3,M,N是斜边AB上的两个动点,且MN=2,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围为( )
| A. | $[2,\frac{5}{2}]$ | B. | [4,6] | C. | $[\frac{119}{25},\frac{48}{5}]$ | D. | $[\frac{144}{25},\frac{53}{5}]$ |
13.已知2a=3b=m,且a,ab,b成等差数列,a,b为正数,则m=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |
 体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].
体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].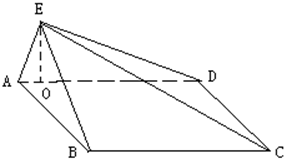 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.