题目内容
17.求函数$f(x)=6-12x+{x^3},x∈[-\frac{1}{3},1]$的最值以及对应的x的值.分析 求导数f′(x),利用导数判断f(x)的单调性,由单调性求函数最值.
解答 解:函数的f′(x)=-12+3x2=3(x+2)(x-2),f′(x)=0,可得x=-2或x=2.
当-$\frac{1}{3}$<x≤1时,f′(x)<0,f(x)递减;
所以当x=-$\frac{1}{3}$时f(x)取得极大值,即最大值;
最大值为:f(-$\frac{1}{3}$)=$\frac{269}{27}$.
x=1时,函数取得最小值f(1),
所以f(x)的最小值为f(1)=-5.
点评 本题考查利用导数求闭区间上函数的最值,属中档题.

练习册系列答案
相关题目
2.已知$\overrightarrow a=(1\;,\;3)$,$\overrightarrow b=(-2\;,\;5)$,则$3\overrightarrow a-2\overrightarrow b$=( )
| A. | (2,7) | B. | (13,-7) | C. | (7,-1) | D. | (-1,-1) |
7.随机变量X服从正态分布(3,σ2),且P(X≤4)=0.84,则P(2<X<4)=( )
| A. | 0.16 | B. | 0.32 | C. | 0.68 | D. | 0.84 |
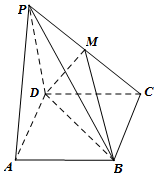 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,且△PAD是边长为2的等边三角形,$PC=\sqrt{13}$,点M是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,且△PAD是边长为2的等边三角形,$PC=\sqrt{13}$,点M是PC的中点.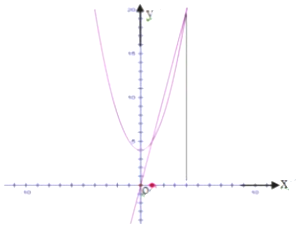
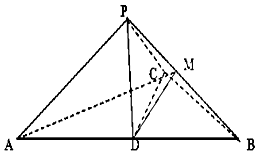 如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为
如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为