如图.由曲线y=x2+4与直线y=5x所围成平面图形的面积．题目和参考答案——青夏教育精英家教网—

题目内容

9．如图，由曲线y=x²+4与直线y=5x所围成平面图形的面积．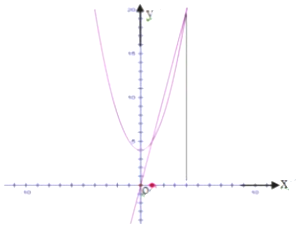

分析首先利用定积分表示封闭图形底面积，然后计算定积分．

解答解：由曲线y=x²+4与直线y=5x所围成平面图形的面积为${∫}_{1}^{4}（5x-{x}^{2}-4）dx$=（$\frac{5}{2}{x}^{2}-\frac{1}{3}{x}^{3}-4x$）|${\;}_{1}^{4}$=$\frac{27}{6}$=$\frac{9}{2}$；

点评本题考查了定积分的几何意义的运用；关键是正确利用定积分表示面积．

练习册系列答案

寒假新生活系列答案

寒假集训合肥工业大学出版社系列答案

寒假作业沈阳出版社系列答案

快乐天天练假期作业寒安徽师范大学出版社系列答案

走进寒假假期快乐练电子科技大学出版社系列答案

1．已知f（x）是定义在[m，n]上的函数，记F（x）=f（x）-（ax+b），|F（x）|的最大值为M（a，b）．若存在m≤x₁＜x₂＜x₃≤n，满足|F（x₁）|=M（a，b），F（x₂）=-F（x₁）．F（x₃）=F（x₁），则称一次函数y=ax+b是f（x）的“逼近函数”，此时的M（a，b）称为f（x）在[m，n]上的“逼近确界”．
（1）验证：y=4x-1是g（x）=2x²，x∈[0，2]的“逼近函数”；
（2）已知f（x）=$\sqrt{x}$，x∈[0，4]，F（0）=F（4）=-M（a，b）．若y=ax+b是f（x）的“逼近函数”，求a，b的值；
（3）已知f（x）=$\sqrt{x}$，x∈[0，4]的逼近确界为$\frac{1}{4}$，求证：对任意常数a，b，M（a，b）≥$\frac{1}{4}$．

17．求函数$f（x）=6-12x+{x^3}，x∈[-\frac{1}{3}，1]$的最值以及对应的x的值．

4．已知抛物线的顶点在坐标原点，对称轴是x轴，顶点与焦点的距离等于4．
（1）求抛物线的方程
（2）若等边三角形的一个顶点位于原点，另外两个顶点在抛物线上，求这个等边三角形的边长．

14．若a＜0＜b，且$\frac{1}{a}＞-\frac{1}{b}$，则下列不等式：①|b|＞|a|；②a+b＞0；③$\frac{b}{a}+\frac{a}{b}＜-2$；④$a＞2b-\frac{a^2}{b}$中，正确的不等式有（　　）

1．已知随机变量X～B（9，$\frac{2}{3}$），Y=2X-1，则D（Y）=8．

18．若a＞0，b＞0，且2a+b=1，则2$\sqrt{ab}$-4a²-b²的最大值是$\frac{\sqrt{2}-1}{2}$．

19．已知函数f（x）=cos（x+ϕ）（-π＜ϕ＜0），g（x）=f（x）+f'（x）是偶函数．
（Ⅰ）求ϕ的值；
（Ⅱ）求函数y=f（x）•g（x）在区间$[{0，\frac{π}{2}}]$的最大值．

试题分类