题目内容
 某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)(Ⅰ)应收集多少位女生样本数据?
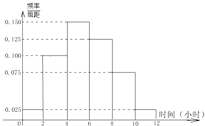
(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4个小时的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由分层抽样的特点可得;(Ⅱ)由频率分布直方图的意义可得.
解答:
解:(Ⅰ)由题意可得300×
=90,
∴应收集90位女生的样本数据.
(Ⅱ)由频率分布直方图得1-2×(0.100+0.025)=0.75,
∴该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75
| 4500 |
| 15000 |
∴应收集90位女生的样本数据.
(Ⅱ)由频率分布直方图得1-2×(0.100+0.025)=0.75,
∴该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75
点评:本题考查概率与统计,涉及频率分布直方图,属基础题.

练习册系列答案
相关题目
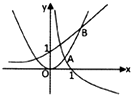 已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )
已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )| A、xa>bx>logcx |
| B、bx>logcx>xa |
| C、logcx>xa>bx |
| D、bx>xa>logcx |
 某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为
某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为