题目内容
设k为整数，化简
．
| sin(kπ-α)cos[(k-1)π-α] |
| sin[(k+1)π+α]cos(kπ+α) |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：分k为偶数和奇数两种情况，分别利用诱导公式进行化简求值．
解答：
解：当k为偶数时，
=
=-1．
当k为奇数时，
=
=-1，
综上可得，
=-1．
| sin(kπ-α)cos[(k-1)π-α] |
| sin[(k+1)π+α]cos(kπ+α) |
| sin(-α)•(-cosα) |
| -sinα•cosα |
当k为奇数时，
| sin(kπ-α)cos[(k-1)π-α] |
| sin[(k+1)π+α]cos(kπ+α) |
| sinα•cosα |
| sinα•(-cosα) |
综上可得，
| sin(kπ-α)cos[(k-1)π-α] |
| sin[(k+1)π+α]cos(kπ+α) |
点评：本题主要考查利用诱导公式进行化简求值，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
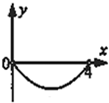
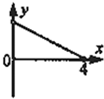
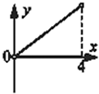
如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点，现将△PCD沿PD翻折，得到△PFD；作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）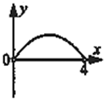
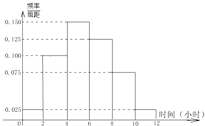某高校共有15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）