题目内容
若圆C的方程为:
(θ为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,则圆C的圆心极坐标为 .(极角范围为[0,2π))
|
考点:简单曲线的极坐标方程,圆的参数方程
专题:坐标系和参数方程
分析:把参数方程化为直角坐标方程,求出圆心的直角坐标,再把圆心的直角坐标化为极坐标.
解答:
解:把圆C的方程为:
(θ为参数)消去参数,化为直角坐标方程为(x-1)2+(y-1)2=1,
表示以(1,1)为圆心、半径等于1的圆.
把圆心的直角坐标化为极坐标为(
,
).
故答案为:(
,
).
|
表示以(1,1)为圆心、半径等于1的圆.
把圆心的直角坐标化为极坐标为(
| 2 |
| π |
| 4 |
故答案为:(
| 2 |
| π |
| 4 |
点评:本题主要考查把参数方程化为直角坐标方程的方法,把点的直角坐标化为极坐标,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
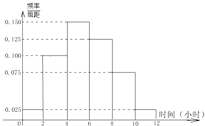 某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)